УРОК №100
02.2023г. ГРУППА
303.МАТЕМАТИКА. «РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ»
Логарифмом
положительного числа b по положительному и отличному от 1 основанию а,
называется показатель степени, в которую надо возвести а, чтобы получить число
b .
log 4 x = 2 (x =
16 )
log 5 x = - 2 (x =
1/25 )
log 0,5 x = 2 (x =
1/4 )
log x 4 = 2 (x =
2 )
log x 5 = 1 (x = 5 )
log x ( - 4) = (- 4) ( решений нет )
log x 1 = 0 (x – любое положительное, х больше или
равно 1 )
Действие нахождения
логарифма числа называют логарифмированием.
Действие нахождения числа по его логарифму называется потенцированием.
При
выполнении преобразований выражений, содержащих логарифмы, при вычислениях и
при решении уравнений часто используют различные свойства логарифмов.
Основные свойства и формулы логарифмов
Логарифм единицы 1. loga1 = 0 ⇔ a>0, a≠1
Логарифм основания 2. logaa = 1 ⇔
a>0, a≠1
Логарифм произведения 3. loga(b⋅c) = loga b + loga c ⇔ a>0, b>0, c>0,a≠1
Логарифм частного 4. logabc=logab—logac ⇔ a>0, b>0, c>0,a≠1
Логарифм степени 5. logabn = n⋅loga b ⇔ a>0, b>0, a≠1
Основное
логарифмическое тождество 6. aloga b = b ⇔ a>0, b>0, a≠1
Основные методы решения логарифмических уравнений:
1. Согласно определению логарифма
Loga x =
b x= ab
Log1/ 2 (2x -4) =-2
Log1 /2 (2x-4) =-2 2x-4=(1/ 2)-2
2x-4 =4
2x=8 2x-4≥ 0
X=4
2. Новая переменная- log23 x- 2log3 x -3 =0
x≥0
Пусть log 3x = у, тогда получим уравнение:
У2 – 2у -3 =0; Решаем квадратное уравнение: и находим корни: х1=3; х2=1
Log 3x =3
Log 3x =-1
Находим корни
х1 = 33 =27;
х2 =3-1 =1/3
Ответ; 27; 1/3
3. Приведение логарифмов к одинаковому основанию.
Log 3
х -2log 1 3x=6
x
Log 3x
+2log3 x =6
3log3 x =6
Log3 x =2
X =32 =9
АЛГОРИТМ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ
1. Сделать справа и слева от знака равенства логарифмы
по одному основанию, избавившись от коэффициентов перед логарифмами, используя
свойства логарифмов.
2. Избавиться от логарифмов, используя правило
потенцирования, остаются только числа, которые были под знаком логарифма.
3. Решаем получившееся обычное уравнение, находим
корни уравнения.
4. Делаем проверку
5. Записываем ответ.
Примеры решения
1.log 2(7-х) =5
По определению:
7-х =25;
7-х=32;
7-х-32=-25
x= -25
Проверка:
log 2(7- (-25) =5
Log 232 =5
5=5
Ответ; х=-25
2. log4 (2-x) =log16 25
Log4 (2-x) =log 25-1
2
Log 4(2-x) = log 45
2-x =5
X=-3
Проверка: log 4(2-(-3)
=log 1625
Log 45= log4 5 Ответ: х=-3
3. log 2(4-x) =8; по определению:
4-х = 28
4-х =256
-х =256-4
-х = 252
Х = -252
Проверка: log 2(4
+252) =8
Log2 256 = 8
28 =256
ЗАДАНИЕ:

Решить следующие логарифмические уравнения
УРОК №99
01.02.2023г. ГРУППА
303. МАТЕМАТИКА. ТЕМА «ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ»
Показательными называют такие уравнения, в которых
неизвестное содержится в показателе степени.
ах=b
 При решении показательных
уравнений используются свойства
степеней, вспомним некоторые из них:
При решении показательных
уравнений используются свойства
степеней, вспомним некоторые из них:
1. При умножении степеней
с одинаковыми основаниями основание остается прежним, а показатели
складываются.
an⋅am=an+m
2. При делении степеней с
одинаковыми основаниями основание остается прежним, а показатели вычитаются
an:am= an-m
3. При возведении степени
в степень основание остается прежним, а показатели перемножаются
(an)m=amn
4. При возведении в
степень произведения в эту степень возводится каждый множитель
(a·b)n=an·bn
5. При возведении в
степень дроби в эту степень возводиться числитель и знаменатель
(a/b)n=an/ bn
6. При возведении любого
основания в нулевой показатель степени результат равен единице
a0=1
7. Основание в любом
отрицательном показателе степени можно представить в виде основания в таком же
положительном показателе степени, изменив положение основания относительно
черты дроби
a-n=1/an
a-n bk=bk/an
8. Радикал (корень) можно
представить в виде степени с дробным показателем
ak/ n =akn
Показательные уравнения
часто сводятся к решению уравнения aх=am, где, а>0,a≠1, x - неизвестное. Для решения таких
уравнений воспользуемся свойством степеней: степени с одинаковым основанием (а>0,a≠1) равны только тогда, когда
равны их показатели.
Решить уравнение 25·5х=1
Решение:
В левой части уравнения
необходимо сделать одну степень с основанием 5 и в правой части уравнения
представить число 1 в виде степени с основанием 5
52·5х=50
При умножении степеней с
одинаковыми основаниями основание остается прежним, а показатели складываются
52+х=50 Далеее проговар в аем: степени с одинаковым основанием (а>0,a≠1) равны только тогда, когда равны их показатели
2+х=0
х= −2
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
САМОСТОЯТЕЛЬНАЯ РАБОТА
ВЫПОЛНИТЕ ТОЛЬКО ПЕРВУЮ ЧАСТЬ

УРОК № 98
01.02.2023г. ГРУППА 303. МАТЕМАТИКА. ТЕМА
«ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ»
Уравнения, в
которых переменная содержится под знаком корня, называются иррациональными.
Какие из
следующих уравнений являются иррациональными?

Метод решения:
При решении иррациональных
уравнений почти всегда необходимо избавиться от радикалов.
Один из возможных методов состоит в
том, что корень из выражения с переменой переносится в одну из частей
равенства, а все остальные выражения в другую (уединение радикала).
После уединения
выполняется возведение в квадрат, в куб или в другую степень.
При решении
уравнения переходим к уравнению-следствию, проверка должна входить в решение
как обязательная часть.
Проверка
может осуществляться различными способами:
1. Каждый из найденных корней
уравнения-следствия подставить в исходное уравнение и проверить, является ли он
корнем исходного уравнения.
2. “Вспомнить” все неравенства, которые
надо было включать в систему, чтобы переходы были равносильными, и проверить
выполняются ли для найденных “корней” эти неравенства.
Сегодня мы
разбираем только уравнения первого способа.
Перед вами 3
иррациональных уравнения. Попробуем их
решить 
 Решение:
Решение:



Далее
давайте попробуем разобрать решение более сложных уравнений
Давайте вместе решим уравнения

Проверка
усвоения учащимися материала на оценку “3” .РЕШИТЕ ПО ВЫБОРУ. С ПРОВЕРКОЙ ![]()
Решение:
Проверка
усвоения учащимися материала на оценку “4” и “5

Решения:
Оценка “5” - решены 5,6 уравнения, если нет решения 5,6 уравнения, то оценка “4”.

УРОК №97
31.01.2023г. ГРУППА 303.
МАТЕМАТИКА.ТЕМА. «РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ»
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член. Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac
А вот свойства дискриминанта:
если D < 0, корней нет;
если D = 0, есть один корень;
если D > 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который
стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы Давайте-ка на примерах — вот у нас есть два уравнения:
x2 — 2x + 6 = 0
x2 — x — 1/4 = 0
В каждом из них старший
коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит
уравнение называется приведенным.
2x2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это не приведенное квадратное уравнение.
Каждое не приведенное
квадратное уравнение можно преобразовать в приведенное, если произвести
равносильное преобразование — разделить обе его части на первый коэффициент.
Запоминаем!
У преобразованного
уравнения те же корни, что и у первоначального. Ну, или вообще нет корней.
Пример 1.
Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе
части исходного уравнения на старший коэффициент 8: 8 +20 8 9 8=0
делим обе части исходного
уравнения на старший коэффициент 8
х2 +2, х 1,12
Ответ:
равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного
уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx +
c = 0 было именно квадратным. Если a =
0, то уравнение обретет вид линейного:
bx + c = 0.
Что касается коэффициентов
b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком
случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение — это квадратное уравнение вида ax2 + bx +
c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны
от нуля.
Для самых любопытных
объясняем, откуда появились такие названия:
Если b = 0, то квадратное уравнение
принимает вид ax2 + 0x+c=0 и оно равносильно ax2 + c = 0.
Если c = 0, то квадратное уравнение
выглядит так ax2 + bx + 0 = 0, иначе его можно написать как ax2
+ bx = 0.
Если b = 0 и c = 0, то квадратное уравнение
выглядит так ax2 = 0.
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три
вида неполных квадратных уравнений:
аx2 = 0, ему отвечают коэффициенты
b = 0 и c = 0;
ax2 + c = 0, при b = 0;
ax2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные
квадратные уравнения по видам.
Как решить уравнение ax2 = 0
Начнем с решения неполных
квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2
= 0.
Уравнение ax2 = 0 равносильно x2
= 0. Такое преобразование возможно,
когда мы разделили обе части на некое число a, которое не равно нулю. Корнем
уравнения x2 = 0 является нуль, так как 02 = 0. Других
корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax2
= 0 имеет единственный корень x = 0.
Пример 1.
Решить −6x2 = 0.
Как решаем:
Замечаем, что данному
уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:
−6x2 = 0
X2 = 0
x = √0
x = 0
Ответ: 0.
Как решить уравнение ax2 + с = 0
Обратим внимание на неполные
квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы
давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы
переносим их из одной части уравнения в другую, они надевает куртку на другую
сторону — меняют знак на противоположный.
Еще мы знаем, что если обе
части уравнения поделить на одно и то же число (кроме нуля) — у нас получится
равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и
колдуем над неполным квадратным уравнением (производим «равносильные
преобразования»): ax2 + c = 0:
1. перенесем c в правую часть: ax2 =
- c,
2.
разделим обе части на a:
x2 = - c/а.
Ну все, теперь мы готовы к
выводам о корнях неполного квадратного уравнения. В зависимости от значений a и
c, выражение — c/а может быть отрицательным или положительным. Разберем
конкретные случаи.
1. Если — c/а < 0, то
уравнение x2 = - c/а не имеет корней. Все потому, что квадрат любого
числа всегда равен неотрицательному числу. Из этого следует, что при — c/а <
0 ни для какого числа p равенство р2 = - c/а не является верным.
2. Если — c/а > 0, то
корни уравнения x2 = - c/а будут другими.
Например, можно
использовать правило квадратного корня и тогда корень уравнения равен числу √-
c/а, так как (√- c/а)2 = - c/а. Кроме того, корнем уравнения может стать
-√- c/а, так как (-√- c/а)2 = - c/а. Ура, больше у этого уравнения
нет корней.
В двух словах
Неполное квадратное уравнение ax2 + c = 0
равносильно уравнению х2= -c/a, которое:
1. не имеет корней при —
c/а < 0;
2. имеет два корня х = √- c/а и х = -√- c/а при
— c/а > 0.
Пример 1. Найти решение
уравнения 8x2 + 5 = 0.
Как решать:
1. Перенесем свободный член в правую часть:
8x2 = - 5
2.Разделим обе части на 8:
X2 = - 5/8
В правой части осталось число со знаком
минус, значит у данного уравнения нет корней.
Ответ:
уравнение 8x2 + 5 = 0 не имеет корней.
2. Как решить уравнение ax2 + bx = 0
Осталось разобрать третий
вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
1. Разложим на множители многочлен, который
расположен в левой части уравнения — вынесем за скобки общий множитель x.
Х(ах+b) =0
Теперь можем перейти от исходного уравнения
к равносильному x ∙(ax + b) = 0. А это уравнение равносильно совокупности двух
уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное
квадратное уравнение ax2 + bx = 0 имеет два корня:
X1 = 0;
Х2 = −b/a.
Пример 1. Решить уравнение 0,5x2 + 0,125x = 0
Как решать:
1. Вынести х за скобки
х(0,5x + 0,125) = 0
Это уравнение равносильно х = 0 и 0,5x
+ 0,125 = 0.
2.
Решить линейное уравнение:
0,5x = −0,125,
х = −0,125/0,5
Разделить:
х = −0,25
Значит
корни исходного уравнения — 0 и −0,25.
Ответ: х = 0 и х = −0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета
можно получить формулу разложения квадратного трехчлена на множители. Выглядит
она так:
Если x1 и x2 — корни квадратного трехчлена ax2 + bx + c, то справедливо равенство ax2 + bx + c = a (x – x1) (x – x2).
Формула разложения
квадратного трехчлена
Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
1.вычислить его значение дискриминанта по
формуле D = b2−4ac;
2. если дискриминант отрицательный,
зафиксировать, что действительных корней нет;
3. если дискриминант равен нулю, вычислить
единственный корень уравнения по формуле х = −b/2a;
4.
если дискриминант положительный, найти два действительных корня
квадратного уравнения по формуле корней формула корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные
уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x2 + 28x — 49 = 0.
Как решаем:
1. Найдем дискриминант: D = 282 —
4(-4)(-49) = 784 — 784 = 0
Так как дискриминант равен нулю, значит это
квадратное уравнение имеет единственный корень
2.
Найдем корень
х = - 28/2(-4)
х = 3,5
Ответ:
единственный корень 3,5.
Пример 2.
Решить уравнение 54 — 6x2 = 0.
Как решаем:
1. Произведем равносильные преобразования.
Умножим обе части на −1
54 — 6x2 = 0 | (-1)
6x2 — 54 = 0
2.
Оставим неизвестное в одной части, остальное перенесем с противоположным
знаком в другую
6x2 = 54
Х2 = 9
х = ±√9
х1 = 3, х2 = - 3
Ответ: два
корня 3 и — 3.
Пример 3. Решить уравнение x2— х = 0.
Как решаем:
1. Преобразуем уравнение
так, чтобы появились множители
х(х — 1) = 0
х₁ = 0, х₂ =
1
Ответ: два
корня 0 и 1.
Пример 4.
Решить уравнение x2— 10 = 39.
Как решаем:
1. Оставим неизвестное в
одной части, остальное перенесем с противоположным знаком в другую
X2— 10 = 39
X2= 39 + 10
X2= 49
х = ±√49
х₁ = 7, х₂ = −7
Ответ: два
корня 7 и −7.
Пример 5.
Решить уравнение 3x2— 4x+94 = 0.
Как решаем:
1. Найдем дискриминант по
формуле
D = (-4)2 — 4 ∙
3 ∙ 94 = 16 — 1128 = −1112
Дискриминант
отрицательный, поэтому корней нет.
Ответ:
корней нет.
. Если дискриминант
отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула поиска действительных корней
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Сумма корней x2 + bx + c = 0
равна второму коэффициенту с противоположным знаком, а произведение корней равняется
свободному члену.
Если дано x2 +
bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
справедливые равенства для
теоремы Виета
1.Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.
Пока неизвестно, какие
корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что
сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен
четырем, значит будем использовать минус четыре:
формула: сумма корней минус 4
х1 + х2 = 4
Произведение корней по
теореме соответствует свободному члену. В данном случае свободным членом
является число три. Значит:
к сумме корней добавляем
произведение корней
х1∙х2
=3
Необходимо проверить равна
ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2
+ 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
поиск корней уравнения.
Получилось, что корнями уравнения являются
числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным
знаком, а значит решение верное.
Произведение корней −1 и
−3 по теореме Виета должно равняться свободному члену, то есть числу 3.
Это условие также
выполняется:
Результат проделанных
вычислений в том, что мы убедились в справедливости выражения:
сумма и произведение корней найдены верно
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и
x2 таковы, что их сумма равна второму коэффициенту уравнения x2
+ bx + c = 0, взятому с противоположным знаком, а их произведение равно
свободному члену, то эти числа и есть корни x2 + bx + c = 0.
Пример 1. Решить при помощи теоремы Виета: x2 − 6x + 8 = 0.
Как решаем:
1. Для начала запишем
сумму и произведение корней уравнения. Сумма будет равна 6, так как второй
коэффициент равен −6. А произведение корней равно 8.
Когда у нас есть эти два равенства, можно
подобрать подходящие корни, которые будут удовлетворять обоим равенствам
системы.
Чтобы проще подобрать корни, нужно их
перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8.
Но значения x1 и x2 надо подбирать так, чтобы они
удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не
подходят, так как они не удовлетворяют равенству x1 + x2
= 6. А значения 4 и 2 подходят обоим
равенствам:
проверка значений 4 и 2 на удовлетворение равенствам
Значит числа 4 и 2 — корни уравнения x2
− 6x + 8 = 0.
А теперь, пожалуйста, РЕШИТЕ СЛЕДУЮЩИЕ КВАДРАТНЫЕ УРАВНЕНИЯ.
Воспользуйтесь сообщением!
УРОК №96
27.01.2023г. ГРУППА 303. ФИЗИКА.
ТЕМА. «РЕШЕНИЕ УРАВНЕНИЙ. ЛИНЕЙНЫЕ УРАВНЕНИЯ»
Тема «Уравнения» - одна из важнейших тем
курса алгебры. Вспомним основные определения и правила.
Устная работа.
- Что называют решением уравнения? (Решением уравнения называют то значение
переменной, при котором данное уравнение обращается в верное равенство.)
- Что значит – решить уравнение? (Решить уравнение – это значит найти все его
корни или доказать, что корней нет.)
- Что называют областью допустимых значений переменной (ОДЗ)? (ОДЗ переменной
уравнения ![]() называют множество тех значений
переменной х, при которых одновременно имеют смысл выражения
называют множество тех значений
переменной х, при которых одновременно имеют смысл выражения ![]() и
и ![]() .)
.)
- Какие
уравнения называются равносильными?
- Какие преобразования приводят к равносильным уравнениям? (Прибавление к обеим
частям уравнения одного и того же числа, умножение обеих частей уравнения на
одно и то же число, деление обеих частей уравнения на одно и то же число не
равное нулю.)
- Какие действия при преобразовании уравнений можно назвать «опасными» и
почему? (Деление уравнения на выражение, содержащее переменную - при этом может
произойти потеря корней и возведение обеих частей уравнения в квадрат - при
этом могут появиться посторонние корни.)
Виды уравнений:
- линейные - квадратные - дробные рациональные - иррациональные -
тригонометрические - логарифмические - показательные
Основные методы решения: Метод
замены. Разложение на множители. Введение новой переменной.
Функционально-графический.
Полезная информация:
1. Для линейного
уравнения ax+b=0, если а=0, то
уравнение корней не имеет. Например, 0х=7.
2. Для квадратного
уравнения ax2 + bx + c = 0, a≠ 0:
если ![]() , то уравнение имеет
два различных действительных корня;
, то уравнение имеет
два различных действительных корня;
если ![]() ,
то уравнение имеет один действительный корень кратности 2;
,
то уравнение имеет один действительный корень кратности 2;
если ![]() ,
то уравнение действительных корней не имеет.
,
то уравнение действительных корней не имеет.
3.Для иррационального уравнения![]() :
:
Метод решения иррациональных уравнений - освобождения
от радикалов путем возведения обеих частей уравнения в соответствующую
натуральную степень. При возведении обеих частей уравнения в нечетную степень
полученное уравнение, равносильно исходному, а при возведении обеих частей
уравнения в четную степень полученное уравнение будет неравносильно исходному
уравнению, при этом могут появиться «лишние» корни.Поэтому при решении
иррациональных уравнений нужно указывать ОДЗ или делать проверку.
4. Для показательного уравнения![]() , (a>0, а≠1):
, (a>0, а≠1):
Одним из самых простых приёмов решения показательных
уравнений является метод сведения обеих частей уравнения к одному основанию (a>0,
а≠1).
5. Для логарифмических уравнений![]() :
:
Одним из самых простых приёмов решения логарифмических
уравнений является использование определения логарифма: logaf(x)
= с, (f(x) >0, a>0, а≠1), где f(x)= ас. При решении
логарифмических уравнений нужно указывать ОДЗ или делать проверку.
6. Для тригонометрических
уравнений:
![]() = m, если -1 ≤ m ≤1, то решения уравнения имеют
вид: x =
= m, если -1 ≤ m ≤1, то решения уравнения имеют
вид: x = ![]() arc
arc![]() + πn, n€Z;
+ πn, n€Z;
![]() = m, если -1 ≤ m ≤1, то
решения уравнения имеют вид: x = ±arccosm + 2πn, n€Z;
= m, если -1 ≤ m ≤1, то
решения уравнения имеют вид: x = ±arccosm + 2πn, n€Z;
tgx = m, то решения уравнения
имеют вид: x = ±arctgm + πn, n€Z
РЕШЕНИЕ УРАВНЕНИЙ
1. Линейные
уравнения
Чтобы научиться решать
простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак
на противоположный. Для примера
рассмотрим простейшее уравнение: x+3=5.
Перенесем 3 из левой части
в правую и меняем знак на противоположный.
Х= 5-3=2
Решение уравнения правилом переноса
Можно проверить: 2 + 3 =
5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Как решаем:
Перенесем 5x из правой части в левую. Знак
меняем на противоположный, то есть на минус.
6x - 5x = 10
Приведем подобные и завершим решение.
x = 10
Ответ: x = 10.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же
число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы
не допустить глупых ошибок.
Применим правило при
решении примера: 4x=8.
При неизвестной х стоит
числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение,
нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на
4. Как это выглядит:
4х/4 =8/4
Теперь сократим дроби,
которые у нас получились и завершим решение линейного уравнения:
Х=2
Рассмотрим пример, когда
неизвестная переменная стоит со знаком минус:
-4x = 12
Как решаем:
Разделим обе части на -4, чтобы коэффициент
при неизвестной стал равен единице.
-4x = 12 | : (-4)
x = −3
Ответ: x = −3.
Если знак минус стоит
перед скобками, и по ходу вычислений его убрали — важно не забыть поменять
знаки внутри скобок на противоположные. Этот простой факт позволит не допустить
обидные ошибки.
Напомним,
что не у каждого линейного уравнения есть решение — иногда корней просто нет.
Изредка среди корней может оказаться ноль — ничего страшного, это не значит,
что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных
уравнений немного, нужно запомнить только один алгоритм, который будет
эффективен для любой задачки.
Алгоритм решения простого линейного
уравнения
1. Раскрываем скобки, если
они есть.
2.
Группируем члены, которые содержат неизвестную переменную в одну часть
уравнения, остальные члены — в другую.
3. Приводим подобные члены в каждой части
уравнения.
4. Решаем уравнение, которое получилось: aх =
b. Делим обе части на коэффициент при неизвестном.
Теперь мы знаем,
как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы
чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1.
Как правильно решить уравнение: 6х + 1 = 19.
Решаем так:
1. Переносим 1 из левой
части в правую со знаком минус.
6х = 19 − 1
2. Выполнить вычитание.
6х = 18
3. Разделить обе части на
множитель, стоящий перед переменной х, то есть на 6.
х = 3
Ответ: 3.
Пример 2.
Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.
Решаем так:
1. Раскрыть скобки
5х − 15 + 2 = 3х − 12 + 2х − 1
2. Сгруппировать в левой части члены с
неизвестными, а в правой — свободные члены. Не забываем при переносе из одной
части уравнения в другую поменять знаки на противоположные у переносимых
членов.
5х − 3х − 2х = −12 − 1 +
15 − 2
Приведем подобные члены.
0х = 0
Ответ: х — любое число.
Пример 3.
Решить: 4х = 1/8.
Решаем так:
1. Разделим обе части
уравнения на множитель стоящий перед переменной х, то есть на 4.
х = 1/8 : 4
х = 1/32
Ответ: 1/32.
Пример 4.
Решить: 4(х + 2) = 6 − 7х.
Решаем так:
4х + 8 = 6 − 7х
4х + 7х = 6 − 8
11х = −2
х = −2 : 11
х = −2/11
Ответ: −2/11 или −(0,18).
О десятичных дробях можно почитать в другой нашей статье.
Пример 5.
Решить: 3(3х - 4) = 4 · 7х + 24
Решаем так:
3(3х - 4) = 4 · 7х + 24
9х - 12 = 28х + 24
9х - 28х = 24 + 12
-19х = 36
х = 36 : (-19)
х = - 36/19
РЕШИТЬ САМОСТОЯТЕЛЬНО.
1. х + 7 = х + 4.
2. 2(х + 3) = 5 − 7х.
3. -4х + 8= (9х+17)
4. 2х – 9=4(3х-1)
УРОК №95-
26.01.2023г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «ПЛОЩАДЬ ТРЕУГОЛЬНИКА»
Треугольник — не самая популярная фигура в
природе и в нашей обычной жизни. Но ей постоянно пользуются дизайнеры одежды,
ювелиры, архитекторы. И, наверняка, нахождение площади треугольника является их
частой задачей
Основные понятия
Треугольник — это геометрическая фигура, которая
получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной
прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика,
которая дает нам информацию о размере части плоскости, ограниченной замкнутой
геометрической фигурой.
Популярные единицы измерения площади:
- квадратный
миллиметр (мм2);
- квадратный
сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Для решения
задач применяются различные формулы, в зависимости от известных исходных
данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том
числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Формулы площади для любого
треугольника
1. Площадь
треугольника через основание и высоту
S =0,5⋅a⋅h
, где a— основание, h— высота.
треугольник
с отмеченной высотой
2. Площадь треугольника через две
стороны и угол между ними.
S=0,5⋅a⋅b⋅sinα
, где a
, b— стороны, α— угол между
ними.
3. Площадь треугольника через
описанную окружность и стороны
S=(a⋅b⋅ c)/(4⋅R) , где a, b, c— стороны, R— радиус описанной окружности.
4. Площадь треугольника через
вписанную окружность и стороны.
S=r⋅(a+b+c)/2 , где a, b, c— стороны, r— радиус вписанной окружности.
или
S=r⋅p , где p=(a+b+c):2 где p — полупериметр.
5. Площадь треугольника по стороне и
двум прилежащим углам
S=a2⋅(sinα⋅sinβ)2÷sin(α+β) , где a— сторона, α и β— прилежащие углы.
6. Формула Герона для вычисления
площади треугольника
Сначала
необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти
произведение полученных чисел, умножить результат на полупериметр и найти
корень из полученного числа.
S=⋅
Для прямоугольного треугольника
Для
прямоугольного треугольника чаще всего используют одну формулу — половину
произведения катетов. Потому что их всегда можно найти с помощью правил
тригонометрии или теоремы Пифагора.
S=0,5⋅a⋅b , где a, b— катеты.
Площадь треугольника по гипотенузе и
острому углу
S=0,25⋅c2⋅sin(2α)
, где c— гипотенуза, α— любой из прилегающих
острых углов.
Гипотенузой принято называть сторону, которая
лежит напротив прямого угла.
Площадь прямоугольного треугольника
по катету и прилежащему углу
S=0,5⋅a2⋅tgα, где a— катет, α— прилежащий угол.
Катетом принято называть одну из двух
сторон, образующих прямой угол.
Площадь треугольника через гипотенузу
и радиус вписанной окружности
S=r⋅(r+c)
, где c— гипотенуза, r— радиус вписанной
окружности.
Площадь треугольника по отрезкам, на
которые делит вписанная окружность его гипотенузу
S=c1⋅c2 , где c1, c2— части гипотенузы
Площадь прямоугольного треугольника
по формуле Герона
S=(p−a)⋅(p−b) , где a, b— катеты, p— полупериметр, который можно найти по формуле: p=(a+b+c)/2
Для равнобедренного треугольника
Равнобедренным треугольником называют треугольник,
у которого боковые стороны равны.
Ниже мы
покажем разные формулы для площади равнобедренного и равностороннего
треугольника, их редко используют, но их легко вывести самому. Попробуйте
сделать это самостоятельно.
Вычисление площади через основание и
высоту
S=0,5⋅b⋅h , где b— основание, h—
высота, проведенная к основанию.
Площадь через боковые стороны и угол
между ними.
S =0,5⋅a2⋅sinα , где
a— боковая сторона, α— угол между боковыми сторонами.
Площадь равностороннего треугольника
через радиус описанной окружности
S=(3⋅
Площадь равностороннего треугольника
через радиус вписанной окружности
S=3⋅
Площадь равностороннего треугольника через
сторону
S=(
Площадь равностороннего треугольника
через высоту
S=h2/3 , где h— высота.
РЕШЕНИЕ ЗАДАЧ:
1. Дан треугольник АВС. Из вершины С опущена высота,
равная 15, сторона АВ=22. Найти площадь
треугольника.
Дано: Решение:
СД=h=15 S= ½ АВ∙ СД= ½ 22∙ 15 =165
АВ=22
Найти SABC-
2. Дан
прямоугольный треугольник, у которого катеты равны 9 и 4. Найти площадь треугольника.
Дано: Решение:
АВ =9 SABC =1/2АВ∙ АС=1/2∙ 9 ∙4 =18
АС =4
3. Дан равнобедренный треугольник АВС, с углом
АВС=600 и основанием АС=8. Найти площадь треугольника.
Решение: Из вершины В на основание АС
проведём высоту ВД, которая делит основание на две равные части АД=ДС=4, т.е.
треугольник равносторонний, т.к. углы будут по 600 (в треугольнике
сумма всех углов равна 1800).
S =1/2 AC∙ BD = 1/ 2 8 ∙8= 32
В задачах встречаются разные фигуры, и, кажется, что нужны разные формулы. Но на самом деле, зная всего несколько формул для треугольника и пользуясь теоремами и свойствами геометрии, можно найти площадь любой фигуры.
Давайте попробуем:
Найти
площадь фигур, изображённых на рисунках: 2.. а, б, в.
Эта фигура не является ни прямоугольником, ни
квадратом. Но мы можем разделить эту фигуру на два прямоугольника, например,
вот таким образом.
Площадь большего прямоугольника S1
=5 ∙4 =20, а площадь меньшего
ЗАДАНИЕ:
1. Запишите в тетрадь все формулы
определения площади треугольника.
2.Выполните
тест
1. Площадь
прямоугольного треугольника равна ...
- половине
произведения его катетов
-
произведению его катетов удвоенному
-
произведению его катетов
- половине произведения наименьшего катета на
гипотенузу
- половине произведения наибольшего катета на
гипотенузу
2. Если высота
одного треугольника равна высоте другого треугольника, то их площади ...1.относятся как длины сторон, к
которым проведены высоты.
2. равны.
- 3. относятся как длины соответствующих высот.
- 4 относятся как длины смежных сторон.
3. Что больше:
- 1.
произведение катетов или произведение гипотенузы на высоту, проведенную
к ней? - - 2. произведение катетов
- 3.
произведение гипотенузы на высоту
- 4. произведения равны: S = ab/2=ch/2
. Решите:
1. Самостоятельную:
1)Найдите
площадь треугольника, если длина одной из сторон равна 24см. и она в 3
раза больше высоты, проведенной к этой стороне.
2)Найдите
площадь треугольника АВС, если ˂А =30°, АВ=14см, ВС=10см, АС=15см.
3) В
прямоугольном треугольнике один из катетов равен 13, а угол, лежащий напротив
него, равен 45°. Найдите площадь треугольника.
4)Найдите
катеты прямоугольного треугольника, если его площадь равна 10
5) В ∆АВС
угол А равен 45˚, ВС=10 см, а высота ВD делит сторону АС на отрезки AD=6 см,
DC=8 см. Найдите площадь ∆АВС и высоту, проведённую к стороне ВС.
, АС = 6 дм, высота ВД равна 2 дм. Найти
площадь треугольника АВД.°С = 135Ð6) В треугольнике АВС
7) В
равнобедренном треугольнике угол при вершине равен 300, а боковая
сторона 10. Найдите площадь данного треугольника.
8) Площадь
ромба равна 507. Одна из его диагоналей в 6 раз больше другой. Найдите
меньшую диагональ.
9) Найти
площадь квадрата, если его диагональ равна 5 см.
10)Найдите
площадь прямоугольной трапеции, основания которой 16 и18,а боковая сторона
составляет с основанием угол 45°
2. Даны
фигуры. Рассчитайте их площади:
 Давайте попробуем:
Давайте попробуем:
Найти площадь фигур, изображённых на рисунках: 2.. а, б, в.
ЖЕЛАЮ УСПЕХА! Решение этих задач поможет вам сдать ГИА.
. \УРОК № 91-92
Ребята! Цель нашего занятия: повторить и обобщить ваши знания по теме. А дальше закрепить решением задач.
Перед вами таблица, в которой
выписаны все формулы для площадей треугольника. Вы ею пользуетесь при решении
теста и задач. Эти знания вам пригодятся
при сдаче ГИА.
Прямоугольник S =ab
Квадрат S =a2
Параллелограмм S = aha
Треугольник S =1/2aha
Прямоугольный
треугольник S =1/2ab
Ромб
S =1/2d1d2
Равносторонний
треугольник S =
Трапеция S =(a + b)/2 h
Кроме этих формул, пожалуйста,
найдите другие формулы площадей треугольника.
Теоретический тест
|
Вариант 1 |
Вариант 1 |
|
1. Выберите верное утверждение: а) площадь прямоугольника равна произведению его сторон; б) площадь квадрата равна квадрату его стороны; в) площадь прямоугольника равна удвоенному произведению его смежных
сторон. |
1. Выберите верное утверждение: а) площадь квадрата равна произведению его сторон; б) площадь прямоугольника равна произведению его противолежащих сторон; в) площадь прямоугольника равна произведению двух его смежных сторон. |
|
2. Закончите фразу: Площадь ромба равна половине произведения... а) его сторон; б) его стороны и высоты, поведенной к этой стороне; в) его диагоналей |
2. Закончите фразу: Площадь параллелограмма равна произведению ... а) двух его смежных сторон. б) его стороны на высоту, проведенную к этой стороне. в) двух его сторон. |
|
3. По формуле S= a * ha можно вычислить площадь: а) параллелограмма; б) треугольника; в) прямоугольника. |
3. По формуле S= 1/2 * d1 * d2 можно вычислить площадь: а) параллелограмма; б) треугольника; в) ромба. |
|
4. Площадь трапеции с основаниями AB и CD, высотой BH вычисляется по
формуле: а) S= AB : 2 * CD * BH; б) S= (AB+BC) : 2 * BH; в) S= (AB+CD) : 2 * BH. |
4. Площадь трапеции с основаниями BC и AD, высотой CH вычисляется по
формуле: а) S= CH * (BC+AD) : 2 б) S= (AB+BC) * CH : 2; в) S= (BC+CD) * CH : 2. |
|
5. Выберите верное утверждение. Площадь прямоугольного треугольника равна: а) половине произведения его стороны на какую-либо высоту; б) половина произведения его катетов; в) произведению его стороны на проведенную к ней высоту. |
5. Выберите верное утверждение: Площадь треугольника равна: а) половине произведения его сторон; б) половине произведения стороны на высоту, проведенную к этой стороне; в) произведению его стороны на какую-либо его высоту. |
|
6. В треугольниках DEF и TRQ высоты DA и TB равны. Тогда SDEF : STRQ=... а) EF : RQ; б) DE : TR; в) EF : RТ |
6. В треугольниках MNK и DOS высоты NE и OT равны. Тогда SMNK : SDOS=... a) MN : OD; б) MK: DS; в) NK
: OS. |
5 задач с
выбором ответа по готовым рисункам
Основания ВС и АD трапеции АВСD соответственно равны 17 и 21, высота трапеции равна 5 см.. Найти SABCD.
- Найти
площадь параллелограмма АВСD, если АВ=5, ВС=8, высота ВК=4.
- Основания
ВС и АD трапеции АВСD соответственно равны 2 и 16, СD=8, угол D равен 300.
Найти SABCD.
- Диагонали
ромба равны 10 и 16. Найти его площадь.
- Найти
площадь
5 устных задач по готовым рисункам (ПОТРЕНЕРУЙТЕСЬ!)
\ Найти площадь параллелограмма АВСD, если АD=8,1, АС=14, угол САD равен 300.
- Найти
площадь параллелограмма MNPK, если MК=8см, угол М равен 600, N
K=5см, диагональ N K перпендикулярна стороне MN.
- Найти
площадь
- Найти
отношение площадей треугольников АВС и MNP, если АВ=5. АС=3, MN=2, MP=7, а угол
А равен углу М.
- Найти
площадь АВСD, если АВ=СD, угол А равен 450, BH - высота
трапеции, АН=6см, HD=16см
.
. Самостоятельная работа
Вариант 1
1.
Сторона треугольника равна 5см, а высота, проведенная к ней, в 2 раза больше
стороны. Найдите площадь треугольника.
2.
Стороны параллелограмма равны 6см и 8см, а угол между ними равен 30o.
Найдите площадь параллелограмма.
3.
В прямоугольной трапеции основания равны 7см и 11см, большая боковая сторона
составляет с основанием угол45o. Найдите площадь трапеции.
4.
В треугольнике ABC стороны AB и BC соответственно равны 14см и 18см. Сторона AB
продолжена за точку А на отрезок AM, равный AB. Сторона BC продолжена за точку
С на отрезок KC, равный половине BC. Найдите площадь треугольника MBK, если
площадь треугольника ABC равна 126см2.
Вариант 2
1.
Сторона треугольника равна 18см, а высота, проведенная к ней, в 3 раза меньше
стороны. Найдите площадь треугольника.
2.
Стороны параллелограмма равны 4см и 7см, а угол между ними 150o.
Найдите площадь параллелограмма.
3.
В равнобедренной трапеции ABCM большее основание AM равно 20см, высота BH
отсекает от AM отрезок AH, равный 6см. Угол BAM равен 45o. Найдите
площадь трапеции.
4.
В ромбе ABCD на стороне BC отмечена точка K такая, что KC:BK=3 : 1. Найдите
площадь треугольника ABK, если площадь ромба равна 48см2.
ЗАДАНИЕ: 1. решить 4 задачи (уровень
сложности учащийся выбирает самостоятельно);
2.подготовить
презентацию или сообщение о Пифагоре (по желанию).
Уровень А.
1.
Стороны параллелограмма равны 10 см и12 см, а один из углов равен 1500.
Найдите площадь параллелограмма.
2.
Найдите сторону ромба, площадь которого равна 12 кв. см, а высота равна 2,4 см.
3.
Найдите высоту треугольника, если она в 4 раза больше стороны, к которой
проведена, а площадь треугольника равна 72 кв.см.
4.
Высота трапеции равна 7 см, а одно из оснований в 5 раз больше другого. Найдите
основания трапеции, если ее площадь равна 84 кв.см.
Уровень Б.
1.
Периметр параллелограмма равен 36 см. Найдите площадь параллелограмма, если его
высота равна 4 см, а один из углов на 600 меньше прямого.
2.
Найдите периметр ромба, высота которого равна 7 см, а площадь равна 84см2.
3.
В равнобедренной трапеции угол равен 1350, а высота в 3 раза меньше
большего основания. Найдите площадь трапеции, если меньшее основание равно 6
см.
4.
В прямоугольном треугольнике угол равен 450, а высота, проведенная к
гипотенузе равна 9 см. Найдите площадь этого треугольника.
Уровень В.
1.Периметр
параллелограмма равен 66 см. Два угла параллелограмма относятся как 1:5, а две
стороны как 2:9. Найдите площадь этого параллелограмма.
2.Найдите
углы ромба, если его высота 7 см, а площадь равна 98 кв. см.
Найдите
площадь треугольника, одна из сторон которого равна 12 см, а к ней прилежащие
углы равны 300 и 750.
3.В
равнобедренной трапеции с углом, равным 1500, боковая сторона равна
6 см, а площадь трапеции равна 66см2. Найдите периметр трапеции.
Каждый учащийся сам выбирает задание на основе своих знаний.
УРОК № 87-88
19-20.01.2023г. ГРУППА 303.
Сегодня
у нас обобщение темы «Тела вращения».
Цель
– обобщить и систематизировать знания по данной теме. Мы вспомним определения,
формулы, свойства, чертежи, развертки, сечения пяти тел вращения. Итак, какие
же это тела?
Цилиндр, конус, усеченный конус, шар и сфера
Кто-то может ответить, откуда произошли их названия?
Исторические
сведения о телах вращения:
Как
вы думаете, от каких слов произошли слова цилиндр, конус, шар и сфера. Слово
цилиндр произошло от греческого слова, которое означало валик или каток, слово
конус в переводе на русский язык означает сосновая шишка, слово шар или сфера
произошло от слова «сфайра» и в переводе означает мяч.
Когда
стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы.
Для этого применялись катки. И заметили, что перекатка проще, если взять кусок
дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с
одним из важнейших тел – цилиндром.
ПРОВЕРКА ЗНАНИЙ.
1.
Прежде, чем перейти к решению задач давайте ответим на вопросы двух тестов, в
которых будет отражен ранее изученный материал.
Ребята!
Выполняете один вариант и обязательно укажите, какой.
|
1. πR2 |
2. πR2H |
3. 2πRH
|
4. 4πR2 |
5. |
||
|
6. πRl |
7. 2πR
|
8. πR(R+l) |
9. πR3 |
10. π(R+r)l |
||
|
11. πR(H+R) |
12. 2πRl |
13. 2πR(H+R) |
14.
|
15. πR3H
|
||
|
№ |
Вопрос: По какой формуле можно вычислить |
Ответ - № формулы |
||||
|
1 |
Площадь боковой поверхности конуса |
|||||
|
2 |
Площадь сферы |
|||||
|
3 |
Объем конуса |
|||||
|
4 |
Площадь боковой поверхности
цилиндра |
|||||
|
5 |
Объем шара |
|||||
|
6 |
Площадь полной поверхности конуса |
|||||
|
7 |
Объем усеченного конуса |
|||||
|
8 |
Площадь полной поверхности цилиндра |
|||||
|
9 |
Площадь круга |
|||||
|
10 |
Объем цилиндра |
|||||
|
11 |
Площадь боковой поверхности
усеченного конуса |
|||||
|
12 |
Длина окружности |
|||||
Тест по теме: «Тела вращения»
|
Ф.И. |
1 вариант |
|
|
№ |
Вопрос |
Ответ |
|
1 |
Цилиндр нельзя получить вращением |
А)треугольника вокруг одной из
сторон; В) квадрата вокруг одной из сторон; С) прямоугольника вокруг одной из
сторон |
|
2 |
Осевое сечение усеченного конуса |
А) круг; В) равнобокая трапеция; С) прямоугольная трапеция |
|
3 |
Точки А и В принадлежат сфере.
Принадлежат ли этой сфере любая точка отрезка АВ |
А) да В) нет |
|
4 |
Точки А и В принадлежат шару.
Принадлежат ли этому шару любая точка отрезка АВ |
А) да В) нет |
|
5 |
Разверткой боковой поверхности
прямого кругового цилиндра может быть |
А) прямоугольник; В) ромб; С) параллелограмм |
|
6 |
Сечением конуса плоскостью,
перпендикулярной его оси, является |
А) треугольник; В) прямоугольник; С) круг |
|
7 |
Плоскость имеет со сферой только
одну общую точку, если расстояние от центра сферы до плоскости |
А) больше её радиуса; В) меньше её радиуса; С) равно её радиусу |
|
8 |
Разверткой боковой поверхности
прямого кругового конуса является круговой |
А) сегмент В) сектор С) слой |
|
9 |
Сечением шара плоскостью,
проходящей через его диаметр, является |
А) круг В) полукруг С) большой круг |
|
10 |
Цилиндр, в осевом сечении которого
квадрат называется |
А) квадратным В) равносторонним С) правильным |
Тест
по теме: «Тела вращения»
|
Ф.И. |
2 вариант |
|
|
№ |
Вопрос |
Ответ |
|
1 |
Цилиндр получается вращением |
А) треугольника вокруг одной из
сторон; В) прямоугольника вокруг одной из
сторон; С) трапеции вокруг одной из сторон |
|
2 |
Осевое сечение конуса |
А) круг; В) равнобокая трапеция; С) равнобедренный треугольник |
|
3 |
Точки А и В принадлежат сфере.
Точка О центр сферы. Принадлежат ли этой сфере любая точка отрезка ОВ |
А) да В) нет |
|
4 |
Точки А и В принадлежат шару. Точка
О центр шара. Принадлежат ли этому шару любая точка отрезка АО |
А) да В) нет |
|
5 |
Разверткой боковой поверхности
прямого кругового цилиндра может быть |
А) прямоугольник; В) ромб; С) параллелограмм |
|
6 |
Сечением цилиндра плоскостью,
перпендикулярной его оси, является |
А) треугольник; В) прямоугольник; С) круг |
|
7 |
Плоскость, которая имеет со сферой
только одну общую точку, называется |
А) перпендикулярной В) касательной С) секущей |
|
8 |
Разверткой боковой поверхности
прямого кругового конуса является круговой |
А) сегмент В) сектор С) слой |
|
9 |
Сечением шара плоскостью является |
А) круг В) полукруг С) большой круг |
|
10 |
Осевое сечение усеченного конуса |
А) трапеция В) прямоугольная трапеция С) равнобедренная трапеция |
Логические задачи:
Задача №1:
Если
шар, куб и цилиндр будут одновременно пущены вниз по наклонной плоскости, что
первым очутится внизу, а что последним?
Задача №2:
Имеется
сосуд цилиндрической формы. Как, не имея никаких измерительных приборов,
отмерить воды ровно половину сосуда?
Задача №3: (практическая)
Перед
вами шесть стаканов цилиндрической формы, три из них наполненных водой, а три
пустых. Вам надо сделать так чтобы стаканы чередовались, то есть полный,
пустой, полный и так далее. Но стакан в руки можно брать только один раз.
Решение расчётных
задач
Задача №1:
Прямоугольный
треугольник с катетами 3 см и 4 см в первый раз вращается вокруг меньшего
катета, а во второй раз вокруг большего катета. Сравните объемы этих конусов.
Решение
Так
как в первый раз прямоугольный треугольник вращается вокруг меньшего катета, то
H=3см и R=4см. Найдем объем конуса по формуле V=
V=πR2H=π32
∙4= 36π (cм3). Выходит, что объем первого конуса больше
второго на 12 π см2.
Задача №2
Найдите
диаметр шара, объем которого равен 27π см3.
Решение
Формула
объема шара V= πR3
πR3=27π
R3=27
R=3
D=2R=2
∙3=6(cм)
Задача №3:
Измениться
ли объем кругового цилиндра, если радиус его основания увеличить в 2 раза, а
высоту уменьшить в 4 раза.
Решение
V=πR2H
Vнового=π(2R)2=
πR2H. Таким образом, объем цилиндра не измениться.
ЗАДАНИЕ:
1.
Решите задачи (один из вариантов). Не забудьте указать.
УРОК 85-86
18-19.01.2023г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «ПОВТОРЕНИЕ ТЕМЫ «Многогранники»
Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве. Фигуры, изучаемые стереометрией: куб, шар, конус, параллелепипед, пирамида и т.д.
Это слово происходит от древнегреческих слов «stereos» — объёмный, пространственный и «metria» — измерение.
Если поверхности геометрических тел составлены из многоугольников, то такие тела называются многогранниками.
Грани — это многоугольники, из которых состоит многогранник. Две соседние грани не могут лежать в одной плоскости.
Рёбра многогранника— это стороны граней, а вершины — это концы рёбер.
Диагональ многогранника — это отрезок, который соединяет две вершины, не принадлежащие одной грани.
Многогранники бывают выпуклыми и невыпуклыми.
Выпуклый многогранник характеризуется тем, что он расположен по одну сторону от плоскости каждой своей грани. На рисунке выпуклый многогранник — октаэдр. У октаэдра восемь граней, все грани — правильные треугольники.
На рисунке — невыпуклый (вогнутый) многоугольник. Если рассмотреть, например, плоскость треугольника EDC, то, очевидно, часть многоугольника находится по одну сторону, а часть — по другую сторону этой плоскости.
Для дальнейших определений введём понятие параллельных плоскостей и параллельных прямых в пространстве и перпендикулярности прямой и плоскости.
Две плоскости называются параллельными, если они не имеют общих точек.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Прямую называют перпендикулярной к плоскости, если она перпендикулярна к любой прямой в этой плоскости.
Призма
Теперь можем ввести определение призмы.
n-угольной призмой называют многогранник, составленный из двух равных n-угольников, лежащих в параллельных плоскостях, и n-параллелограммов, которые образовались при соединении вершин n-угольников отрезками параллельных прямых.
Равные n-угольники называют основаниями призмы.
Стороны многоугольников называют рёбрами оснований.
Параллелограммы называют боковыми гранями призмы.
Параллельные отрезки называют боковыми рёбрами призмы.
Призмы бывают прямыми и наклонными.
Если основания прямой призмы — правильные многоугольники, то такую призму называют правильной.
У прямых призм все боковые грани — прямоугольники. Боковые рёбра прямой призмы перпендикулярны к плоскостям её оснований.
Если из любой точки одного основания провести перпендикуляр к другому основанию призмы, то этот перпендикуляр называют высотой призмы.
На рисунке — наклонная четырёхугольная призма, в которой проведена высота B1E.
В прямой призме каждое из боковых рёбер является высотой призмы.
На рисунке — прямая треугольная призма. Все боковые грани — прямоугольники, любое боковое ребро можно называть высотой призмы. У треугольной призмы нет диагоналей, так как все вершины соединены рёбрами
На рисунке — правильная четырёхугольная призма. Основания призмы — квадраты. Все диагонали правильной четырёхугольной призмы равны, пересекаются в одной точке и делятся в этой точке пополам.
Четырёхугольная призма, основания которой — параллелограммы, называется параллелепипедом.
Вышеупомянутую правильную четырёхугольную призму можно также называть прямым параллелепипедом.
Если основания прямого параллелепипеда — прямоугольники, то этот параллелепипед — прямоугольный.
На рисунке — прямоугольный параллелепипед. Длины трёх рёбер с общей вершиной называют измерениями прямоугольного параллелепипеда.
Например, AB, AD и AA1 можно называть измерениями.
Так как треугольники ABC и ACC1 — прямоугольные, то, следовательно, квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений:
AC12=AB2+AD2+AA12.
Если через соответственные диагонали оснований провести сечение, получится то, что называют диагональным сечением призмы.
В прямых призмах диагональные сечения являются прямоугольниками. Через равные диагонали проходят равные диагональные сечения.
На рисунке — правильная шестиугольная призма, в которой проведены два разных диагональных сечения, которые проходят через диагонали с разными длинами.
Основные формулы для расчётов в прямых призмах
1. Боковая поверхность Sбок.=Pосн.⋅H, где H — высота призмы. Для наклонных призм площадь каждой боковой грани определяется отдельно.
2. Полная поверхность Sполн.=2⋅Sосн.+Sбок.. Эта формула справедлива для всех призм, не только для прямых.
3. Объём V=Sосн.⋅H. Эта формула справедлива для всех призм, не только для прямых.
Пирамида
n-угольная пирамида — многогранник, составленный из n-угольника в основании и n-треугольников, которые образовались при соединении точки вершины пирамиды со всеми вершинами многоугольника основания.
n-угольник называют основанием пирамиды.
Треугольники — боковые грани пирамиды.
Общая вершина треугольников — вершина пирамиды.
Рёбра, выходящие из вершины — боковые рёбра пирамиды.
Перпендикуляр от вершины пирамиды к плоскости основания называют высотой пирамиды.
На рисунке — шестиугольная пирамида GABCDEF, проведена высота пирамиды GH.
Пирамиду, в основании которой правильный многоугольник, и высота соединяет вершину пирамиды с центром правильного многоугольника, называют правильной.
У правильной пирамиды все боковые грани — равные равнобедренные треугольники. Если провести высоты этих треугольников, то они также будут равны.
Высоту боковой грани правильной пирамиды называют апофемой.
На рисунке — правильная четырёхугольная пирамида. Высота пирамиды KO проведена от вершины K к центру основания O.
Высота боковой грани KN — апофема.
Если у правильной треугольной пирамиды все боковые грани — равносторонние треугольники (равные с основанием), то такую пирамиду называют правильным тетраэдром:
ΔABC=ΔABD=ΔACD=ΔBCDп.
Если у многоугольника в основании есть диагонали, то через эти диагонали и вершину пирамиды можно провести диагональное сечение.
На рисунке проведено диагональное сечение правильной четырёхугольной пирамиды.
Основные формулы для расчётов в правильных пирамидах
1. Боковая поверхность Sбок.=Pосн.⋅h2, где h — апофема. Для пирамид, которые не являются правильными, необходимо определить отдельно поверхность каждой боковой грани.
2. Полная поверхность Sполн.=Sосн.+Sбок.. Эта формула справедлива для всех пирамид, не только для правильных.
3. Объём V=13⋅Sосн.⋅H, где H — высота пирамиды. Эта формула справедлива для всех пирамид, не только для правильных.
ЗАДАНИЕ
1. Оформить конспект сообщения в виде таблицы.
2. Решить задачи.
1. В прямоугольном параллелепипеде стороны основания равны 12см и 5см.
Диагональ параллелепипеда образует с плоскостью основания угол 45 .
Найдите площадь боковой поверхности параллелепипеда
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота 12см. Найдите площадь полной поверхности пирамиды
3. Найдите сторону основания и высоту правильной четырёхугольной призмы, если Sполн=90см2,
Sбок=40см2.
4. В правильной четырёхугольной пирамиде высота равна 12см, а апофема - 15см. Найдите площадь полной поверхности пирамиды.
5. Сторона основания правильной четырёхугольной пирамиды равна 12см, а высота пирамиды 12 см. Найдите боковое ребро пирамиды.
6. В основании прямой призмы ABCDA1B1C1D1 лежит параллелограмм со сторонами 3см и 6см и углом между ними 60. Диагональ B1D образует с плоскостью основания угол 30. Найдите площадь боковой поверхности.
УРОК № 84
18.01.2023г. ГРУППА 303 МАТЕМАТИКА
Контрольная работа № 5 по теме «Элементы комбинаторики и теории вероятностей»
Вариант 1
1. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?
1) 30 2) 100 3) 120 4) 5
2. В 9«Б» классе 32 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
1) 128 2) 35960 3) 36 4)46788
3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
1) 10 2) 60 3) 20 4) 30
4. Вычислить: 6! -5!
1) 600 2) 300 3) 1 4) 1000
5. В ящике находится 45 шариков, из которых 17 белых. Потеряли 2 не белых шарика. Какова вероятность того, что выбранный наугад шарик будет белым?
1)
6. Бросают три монеты. Какова вероятность того, что выпадут два орла и одна решка?
1)
7. В денежно-вещевой лотерее на 1000000 билетов разыгрывается 1200 вещевых и 800 денежных выигрышей. Какова вероятность выигрыша?
1) 0,02 2) 0,00012 3) 0,0008 4)
Вариант 2
1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
1) 100 2) 30 3) 5 4) 120
2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
1) 3 2) 6 3) 2 4) 1
3. Сколькими способами из 9 учебных предметов можно составить расписание учебного дня из 6 различных уроков.
1) 10000 2) 60480 3) 56 4) 39450
4. Вычислите:
1) 2 2) 56 3) 30 4)
5. В игральной колоде 36 карт. Наугад выбирается одна карта. Какова вероятность, что эта карта – туз?
1)
6. Бросают два игральных кубика. Какова вероятность того, что выпадут две четные цифры?
1) 0,25 2)
7. В корзине лежат грибы, среди которых 10% белых и 40% рыжих. Какова вероятность того, что выбранный гриб белый или рыжий?
1) 0,5 2) 0,4 3) 0,04 4) 0,8
УРОК №.84-85
30.12.2023г. . ГРУППА 303.
Тема: Решение практических задач с применением вероятностных методов
ПРАКТИЧЕСКАЯ РАБОТА (Решите самостоятельно)
Вариант 1
1. В урне содержится 10 красных, 15 синих и 5 белых шаров. Из неё вынимается наугад 1 шар. Какова вероятность того, что этот шар не белый?
2. Монету подбросили 2 раза. Найти вероятность того, что оба раза выпадет герб.
3. В урне содержится 5 белых, 6 красных, 7 синих и 4 зелёных шара. Вынимают наугад 1 шар. Какова вероятность того, что этот шар чёрный?
4. Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах?
5. Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 5, 7, 9?
6. В ящике находятся шары с номерами 1, 2, 3, ..., 25. Наугад вынимают один шар. Какова вероятность того, что номер этого шара будет простым числом?
7. Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можно сделать?
Вариант 2
1. Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
2. Найти вероятность того, чтопри бросании двух игральных костей хотя бы один раз выпадет 5 очков.
3. В урне лежат шары, двузначные номера которых составлены из цифр 1,2,3,4,5. Какова вероятность вынуть шар с номером 15?
4. Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 5, 7, 9 без повторения цифр?
5. Из 15 туристов надо выбрать дежурного и его помощника. Сколькими способами это можно сделать?
6. Из 30 книг, стоящих на полке, 5 учебников, а остальные художественные произведения. Наугад берут с полки одну книгу. Какова вероятность того, что она не окажется учебником?
7. Из 9 книг и 6 журналов надо выбрать 2 книги и 3 журнала. Сколькими способами можно сделать этот выбор?
1. Решение заданий записать в тетрадь
Контрольные вопросы
1. Какое событие называют достоверным?
2. Какое событие называют невозможным?
3. Дайте определение противоположных событий.
4. Сформулируйте классическое определение вероятности.
5. Чему равна вероятность достоверного события?
6. Чему равна вероятность невозможного события?
7. Каким неравенствам удовлетворяет вероятность любого события?
8. Что называется относительной частотой события?
9. Сформулируйте теорему умножения событий.
10. Сформулируйте теорему сложения событий.
Решение задач (изучите)
Простейшие задачи на определение вероятности события
Задача 1. В партии из 200 деталей имеется 8 бракованных. Определить вероятность того, что, взятая наугад, деталь окажется стандартной.
Решение: Событие А - взятая наугад деталь стандартная. ?Каким событием является событие А? А - случайное событие. Число всех исходов ![]() , число исходов, благоприятствующих наступлению события А,
, число исходов, благоприятствующих наступлению события А, ![]() Поэтому вероятность события равна
Поэтому вероятность события равна ![]()
Ответ: ![]()
Задача 2. Из пяти букв разрезной азбуки составлено слово «урок». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получится слово «урок».
Решение: Событие А - из рассыпанных букв сложится слово «урок». ?Каким событием является событие А? А – случайное событие. Число всех возможных исходов равно ![]() . Число исходов, благоприятствующих наступлению событию А равно m =1. Вероятность события А равна
. Число исходов, благоприятствующих наступлению событию А равно m =1. Вероятность события А равна![]() .
. ![]() Ответ:
Ответ: ![]() .
.
Задачи на применение теорем сложения и умножения вероятностей
Задача 3. В коробке лежат 8 зеленых, 7 синих и 15 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет, синим или зеленым.
Решение: Событие А - взяли синий карандаш, событие В - взяли зеленый карандаш, событие С - взяли синий или зеленый карандаш. ?Какими событиями являются события А и В? События А и В - несовместимые, поэтому применяем формулу сложения вероятностей. Всего исходов: ![]() .Тогда, найдём вероятности всех событий:
.Тогда, найдём вероятности всех событий:![]() ,
, ![]() , . Ответ:
, . Ответ: ![]()
Задача 4. В первой урне 7 белых и 3 чёрных шара; во второй – 3 белых и 7 чёрных шаров. Из каждой урны наудачу вынимают 1 шар. Какова вероятность того, что оба вынутых шара белые?
Решение: Событие А – вынутый белый шар из первой урны; В – вынутый белый шар из второй урны. ?Какими событиями являются события А и В? События А и В – независимые, поэтому применяем формулу умножения вероятностей независимых событий: ![]() . Число всех исходов
. Число всех исходов ![]() Найдём вероятности событий:
Найдём вероятности событий: ![]() . Тогда
. Тогда ![]() Ответ: 0,21
Ответ: 0,21
УРОК №83
28.12.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА
«Понятие о задачах математической статистики. Представление числовых данных (таблицы, диаграммы, графики). Решение практических задач на обработку числовых данных, вычисление их характеристик».
«Статистика знает все. Известно, сколько какой пищи съедает в год средний гражданин республики… Известно, сколько в стране охотников, балерин… станков, собак всех пород, велосипедов, памятников, маяков и швейных машинок… Как много жизни, полной пыла, страстей и мысли глядит на нас со статистических таблиц!»
И. Ильф, Е. Петров
1) Какие статистические данные вам известны?
2) Каким образом их получают?
3) Можем ли мы с вами получить информацию, обработать ее, применить для своей осведомленности и использовать знания при необходимости?
Давайте вспомним известные вам примеры, в которых информируется об итогах обработанной информации. (Средний прожиточный минимум на данный период, средняя продолжительность жизни, средняя зарплата по области, по стране; средняя успеваемость по группе, по техникуму; среднемесячная температура воздуха и т.д.)
Слово «статистика» в переводе означает: состояние, положение вещей.
1) Какого рода статистика вам известна?
2) О чем нас информируют статистические данные?
- Экономическая статистика изучает производство и потребление разнообразных видов продукции, изменение цен, спроса и предложения на товары, прогнозирует рост и падение производства и потребления, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое
- Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий.
- Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный).
- Есть еще статистика финансовая, налоговая, биологическая и т.д.
1.Статистика – это научное направление (комплекс наук), объединяющее принципы и методы работы с числовыми данными, характеризующими массовые явления.
2. Статистика – это отрасль практической деятельности, направленной на сбор, обработку, анализ статистических данных.
3. Статистика – это совокупность статистических данных, характеризующих какое-нибудь явление или процесс (например, статистика рождаемости и смертности в России, статистика успеваемости учащихся и т.п.).
Математическая статистика – это раздел математики который занимается разработкой методов сбора, описания и анализа экспериментальных результатов наблюдений, массовых случайных явлений..
Математическая статистика – наука, основанная на законах теории вероятностей. Статистические методы обработки данных из самых разных областей жизни имеют много общего. Это позволило создать универсальные научно обоснованные методы статистических исследований и проверки статистических гипотез.
Статистические характеристики – это математические понятия, с помощью которых описываются отличительные особенности и свойства совокупности данных, полученных с помощью наблюдений или каким-то другим способом. Значение характеристик состоит еще и в том, что они «подсказывают», с каких позиций целесообразно анализировать имеющуюся совокупность данных.
Сбор информации: происходит массово или выборочно. При этом используется: перепись населения, отчеты предприятий, текущий учет, опросы, анкетирование, интервьюирование, наблюдения, статистика больниц, загсов и т.д.
Фундаментальными понятиями математической статистики являются генеральная совокупность и выборка. Генеральную совокупность удобно изображать с использованием круговой диаграммы, выборку – с использованием части круговой диаграммы.
Способы образования выборочной совокупности: случайная (отбирая на удачу), механическая (отбирая через определенный интервал), типическая (случайные выборки из каждой группы), серийная (разбивается на непересекающиеся серии или группы).
Обработка собранной информации.
Статистическая информация о результатах наблюдений или экспериментов может быть представлена в различных формах.
Простейшей из них является запись в порядке их появления – запись в ряд,
называемый простым статистическим рядом или выборкой.
Отдельные значения, составляющие этот ряд, называют вариантами или просто данными.
Понятие объема ряда
Количество вариант в ряду n называют объемом ряда, или объемом выборки.
Варианты в ряду могут иметь как различные, так и одинаковые значения.
Понятие ранжированного ряда
Составить ранжированный ряд - это значит записать варианты в порядке их возрастания.
Характеристики числового ряда
Пример 1. Пусть ученик получил в течение года следующие отметки по математике: 5, 2, 4, 5, 5, 4, 4, 5, 5, 5. Какую четвертную отметку поставит ему учитель?
Многих школьников волнует подобная проблема, и чаще всего ученики решают ее следующим естественным образом: складывают все отметки и делят сумму оценок на их количество.
В нашем случае (5 + 2 + 4 + 4 + 5 + 5 + 4 + 4 + 5 + 5 + 5) / 10 = 4,4
Число 4,4, которое получается в результате, называется средним арифметическим. Поскольку такую оценку в журнал ставить не принято, учитель, скорее всего, округлит ее до 4.
Средним арифметическим (или выборочным средним) ряда чисел называется частное от деления суммы этих чисел на их количество: Среднее арифметическое, конечно, является важной характеристикой ряда чисел, в нашем случае — отметок за четверть, но иногда полезно рассматривать и другие средние.
Например, претендуя на «5», ученик наверняка будет использовать такой аргумент: «Чаще всего в четверти я получал пятерки!». Статистик в этом случае сказал бы иначе: «Модой этого ряда является число 5».
Модой (Мо) называют число ряда, которое встречается в этом ряду наиболее часто.
Можно сказать, что оно в этом ряду самое «модное». В отличие от среднего арифметического, которое можно вычислить для любого числового ряда, моды может вообще не быть.
Например, пусть тот же ученик получил по русскому языку следующие отметки: 4, 2, 3, 5. Каждая отметка встречается в этом ряду только один раз, и среди них нет числа, встречающегося чаще других. Значит, у этого ряда нет моды. А вот среднее арифметическое, конечно, есть:(4 + 2 + 3 + 5) : 4 = 3,5.
Такой показатель, как мода, можно использовать не только в числовых рядах. Вы уже знакомы с социологическими опросами. Если, например, опросить большую группу учеников, какой предмет вам нравится больше всего, то модой можно назвать тот предмет, который будут называть чаще остальных. Это одна из причин, по которой мода широко используется при изучении спроса. Например, при решении вопросов, в пачки какого веса фасовать масло, какие открывать авиарейсы и т. п., предварительно изучается спрос и выявляется мода — наиболее часто встречающийся заказ. И даже выборы президента, с точки зрения статистики, не более чем определение моды.
Медиана числового ряда
Медианой ряда, состоящего из нечетного количества чисел, называется число данного ряда, которое окажется посередине, если этот ряд упорядочить: ,
Me =
Медианой ряда, состоящего из четного количества чисел, называется среднее арифметическое двух стоящих посередине чисел этого ряда, если этот ряд упорядочить.,
Me =
Для того чтобы найти медиану ряда чисел, нужно сначала их упорядочить — составит ранжированный ряд (записать в порядке убывания).
Пример 2.В конце года 11 учеников 8 класса сдавали норматив по бегу на 100 метров. Были зафиксированы следующие результаты:
Ученик
Результат(с)
Данила
15,3
Петя
16,9
Лена
21,8
Катя
18,4
Стаc
16,1
Аня
25,1
Оля
19,9
Боря
15,5
Паша
14,7
Наташа
20,2
Миша
15,4
После того как все ребята пробежали дистанцию, к преподавателю подошел Петя и спросил, какой у него результат. «Самый средний результат: 16,9 секунды», — ответил учитель. «Почему? — удивился Петя. — Ведь среднее арифметическое всех результатов — примерно 18,3 секунды, а я пробежал на секунду с лишним лучше. И вообще, результат Кати (18,4) гораздо ближе к среднему, чем мой». «Твой результат средний, потому что пять человек пробежали лучше, чем ты, и пять — хуже. То есть ты как раз посередине», — сказал учитель. На языке статистики результат Пети называется медианой исходного ряда данных.
Для того чтобы найти медиану ряда чисел, нужно сначала их упорядочить — составить ранжированный ряд. В нашем примере он выглядит так:
14,7; 15,3; 15,4; 15,5; 16,1; 16,9; 18,4; 19,9; 20,2; 21,8; 25,1.
Средним (шестым по счету) числом является 16,9: пять чисел меньше него, пять чисел больше. Значит, 16,9 — медиана.
Достоинством медианы является ее большая по сравнению со средним арифметическим «устойчивость к ошибкам».
Представим себе, что в наши наблюдения вкралась досадная оплошность: например, при записи одного из результатов соревнований мы пропустили десятичную запятую и вместо 20,2 написали 202. Тогда среднее арифметическое результатов возрастет с 18,1 секунды до 34,6 секунды, а медиана будет по-прежнему 16,9 секунды!
Медиану используют вместо средней арифметической, когда крайние варианты упорядоченного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.
Числовой ряд иногда удобно представлять в виде таблицы, если имеем большой объем информации и данные повторяются.
Представим ряд данных 5, 2, 4, 5, 5, 4, 4, 5, 5, 5 в виде таблицы
X
2
4
5
M
1
3
6
W
1/10
10
3/10
30
6/10
60
В первой строке – значение случайной величины Х, во второй – частота значений варианты М, в третьей строке – относительная частота появления события.
По табличным данным тоже можно найти объем ряда, среднее арифметическое, моду и медиану.
Объем - сложить все данные М
Мода – самое большое значение М
Медиана - Ме
Среднее арифметическое: = cумме произведений элементов первой строки на частоту появления второй строки, и все поделить на 10:
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений.
Обработанные результаты статистики можно демонстрировать графически.
Пример 3: В первом полугодии 2011 года завод получил прибыль в 10 млн. рублей. Распределение прибыли по месяцам показано в таблице
В координатной плоскости на оси абсцисс будем отмечать номер месяца (янв. – 1, февр. – 2 и т.д.). На оси ординат будем отмечать прибыль завода
(в млн. руб.).
Отметим точки: (1;1,4),(2;1,3),(3;1,5),(4;2,1),(5;2),(6;1,7) и соединим их последовательно отрезками.
Полученную ломаную линию называют полигоном частот.
Графики статистического распределения.
Распределение случайных величин можно задавать и демонстрировать графически.
Гистограмма – помогает наглядно сравнивать по величине несколько объектов.
Полигон частот – показывает промежутки убывания и возрастания, точки максимума и минимума.
Существуют и другие статистические характеристики, которые называются характеристиками отклонения.
Размах. Дисперсия. Среднеквадратичное отклонение
Средние характеристики числового ряда позволяют оценить его поведение «в среднем». Но это далеко не всегда полностью характеризует выборку.
Размах — это разность наибольшего и наименьшего значений ряда данных: …
R =
Пример 4. Температура на Меркурии колеблется от - 150 до + 350 Удобен ли климат Меркурия для жизни людей, если на планете Меркурий средняя температура +15?
Например, на планете Меркурий средняя температура +15°. Исходя из этого статистического показателя, можно подумать, что на Меркурии умеренный климат, удобный для жизни людей.
Однако на самом деле это не так. Температура на Меркурии колеблется от — 150° до +350°.
Значит, чтобы получить представление о поведении числового ряда, помимо средних характеристик надо знать характеристики разброса, показывающие, насколько значения ряда различаются между собой, как сильно они «разбросаны» вокруг средних. Простейшей такой характеристикой является размах.
Для температуры на Меркурии, например, размах равен
350° — (-150°) = 500°. Конечно, такого перепада температур человек выдержать не может.
Размах очень просто вычисляется, но не всегда несет достоверную информацию, так как на его величину может сильно повлиять какое-то одно (возможно, ошибочное) значение статистического ряда.
Вот почему в реальных статистических исследованиях чаще используют другую характеристику разброса, которая сложнее вычисляется, но зато меньше подвержена таким колебаниям.
Прежде чем определять эту величину, рассмотрим на примере, какой самый естественный способ вычисления «среднего отклонения от среднего».
Пример 5. Дан числовой ряд, который представляет собой стоимость одного литра бензина на 10 автозаправочных станциях (в рублях):
32,2; 32,8; 33; 32,9; 33; 32,5; 32,8; 33; 33,2; 32,8.
Найдем среднее арифметическое этих цен:
(32,2 + 32,8 + 33 + 32,9 + 33 + 32,5 + 32,8 + 33+ 33,2 + 32,8 ) / 10 = 32,82.
Самым естественным, на первый взгляд, кажется посчитать отклонение от среднего для каждого члена ряда и затем найти их среднее арифметическое:
((32,2 - 32,82) + (32,8 - 32,82) +(33- 32,82) + … + (32,8 - 32,82)) / 10 = 0.
Мы получили нуль совсем не случайно: при вычислении «среднего разброса» по такой формуле часть отклонений входит в сумму со знаком «плюс», часть — со знаком «минус», а в сумме всегда получается нуль.
Какой же выход? Можно суммировать, например, модули отклонений — тогда уж нуля точно не будет. Иногда так и поступают, но с модулем не всегда удобно работать. Поэтому математики решили, что лучше складывать не модули отклонений, а их квадраты — они ведь тоже неотрицательные.
Так появилось понятие дисперсии числового ряда.
Дисперсией числового ряда называется среднее арифметическое квадратов отклонений от среднего арифметического.
D =
Найдем дисперсию числового ряда из нашего примера с ценами на бензин. Среднее арифметическое мы уже вычислили — оно равно32,82.
Найдем теперь дисперсию, т. е. среднее арифметическое квадратов отклонений от среднего:
((32,2 - 32,82)2 + (32,8 - 32,82)2 + (33 - 32,82)2 + … + (32,8 - 32,82)2 ) / 10 = 0,0736.
У дисперсии есть один существенный недостаток: если исходные значения ряда измеряются в каких-то единицах (например, в рублях), то у дисперсии эти единицы возводятся в квадрат («квадратные» рубли).
В нашем примере среднее значение цены получилось 32 рубля 82 копейки, а вот дисперсия цен — около 7 … «квадратных копеек».
Избавиться от таких странных единиц измерения можно, если использовать другую характеристику разброса — стандартное отклонение.
Стандартным (или средним квадратичным) отклонением числового ряда называется квадратный корень из дисперсии:
Обозначают его греческой буквой
Как и при изучении средних характеристик, попробуем найти характеристики разброса по таблице частот.
Математическое ожидание случайной величины
Как мы знаем, распределение вероятностей случайной величины — это таблица, в которой указаны значения случайной величины и их вероятности. Для практики не всегда нужно изучать всю таблицу распределения. Достаточно знать некоторые ее числовые характеристики. Рассмотрим случайную величину X. Ее математическое ожидание обычно обозначают Е(Х).Пусть распределение вероятностей случайной величины X задано таблицей:
Значение величины X
Х1
Х2
Х3
Хn
Вероятность P1
P2
P3
Pn
Математическим ожиданием случайной величины X называют число
Е(Х)= х1 · Р1 + х2 · Р2 + … + хn · Рn.
Математическое ожидание Е(Х) называют также ожидаемым значением случайной величины X, средним значением случайной величины X. Если значения случайной величины измеряются в каких-либо единицах (например, рост — в сантиметрах, температура — в градусах), то ее математическое ожидание измеряется в этих же единицах (средний рост — в сантиметрах, средняя температура — в градусах)
Пример 6. Для проведения лотереи изготовили 100 билетов. Из них 1 билет с выигрышем в 500 р., 10 билетов с выигрышами по 100 р. и остальные 89 билетов без выигрышей. Наудачу выбирают один билет. Найдем математическое ожидание выигрыша M(X).
Количество билетов
1
10
89
Выигрыш
500 руб.
100 руб.
0 руб
Вероятность
1/100
1/10
89/100
Эта случайная величина может принимать три значения: 500 р., 100 р. и 0 р. (нет выигрыша). Их вероятности равны 0,01, 0,10 и 0,89. Математическое ожидание выигрыша равно 500 · 0,01 + 100 · 0,10 + 0 · 0,89 = 15 (р.). Получается, что средний выигрыш на один билет равен 15 р.
Для того чтобы лотерея приносила доход своим устроителям, цена билета должна быть больше, чем средний выигрыш. Предположим, что билет стоит 20 р. Продав все билеты, устроители лотереи получат 2000 рублей.
На выплату выигрышей будет потрачено 1500 рублей.
Таким образом, доход от лотереи составит 500 рублей.
Разумеется, может случиться так, что на один купленный нами билет мы получим большой выигрыш. Но если бы некто решил купить все билеты, то он достоверно потерял бы 500 рублей — по 5 на каждый из 100 билетов.
Так устроены все лотереи: математическое ожидание выигрыша на один билет меньше цены этого билета.
Это условие является непременным, и оно обеспечивает рентабельность лотереи и доход ее устроителям. Человек, который решил сыграть в лотерею, должен понимать это и сознательно рисковать своими деньгами.
Задача 1. В небольшой фирме 10 сотрудников: 7 рабочих, мастер, бухгалтер, директор. Зарплата у рабочих: 2000, у мастера 4000, у бухгалтера 16000, у директора 40000. Найдите, чему будет равна средняя зарплата на этом предприятии?
Решение:
В этом случае используют другую статистическую характеристику – медиану.
Задача 2. В таблице приведена информация о длине некоторых рек, протекающих по территории Ивановской области, впадающих в реку Волга
9, 34, 45, 54, 58, 132, 152.
а) Найдите среднюю длину рек (среднее арифметическое);(484:7=69,14)
б)Найдите длину рек в среднем (медиану данных=54);
в) Найти размах длины рек (152 - 9=143)
Ответ: а) 69км, б) 54 км, в) 143
Итак, для характеристики статистической информации используют среднее арифметическое и медиану. Во многих случаях одна из характеристик может не иметь никакого содержательного смысла.
Задача 3. В женском обувном магазине провели статистические исследования и составили соответствующую таблицу по цене обуви и количества продаж:
Первый и второй этап статистического исследования уже пройдены: данные собраны и систематизированы. Осталось произвести анализ данных.
Для данных показателей надо найти статистические характеристики и объяснить их значение.
n = 8+9+14+15+3+1=50
= = =1426
Mo = 1500 Mo = 1800
Ме = 1500
После ученики должны ответить на следующие вопросы:
- Из данных ценовых категорий, обувь за какую цену не следует продавать магазину?
- Обувь, по какой цене следует распространять?
- К какой цене лучше стремиться?
По каким параметрам еще можно провести статистические исследования в обувном магазине?
Задача 4. На соревнованиях по фигурному катанию судьи поставили спортсмену следующие оценки:
5,2 5,4 5,5 5,4 5,1 5,1 5,4 5,5 5,3
Для полученного ряда чисел найдите среднее арифметическое, размах, медиану и моду. Что характеризует каждый из этих показателей?
Среднее арифметическое 5,2 характеризует средний уровень оценок.
Размах R = = 5,5 – 5,1=0,4 характеризует разброс оценок.
Мода Мо = 5,4 показывает оценку, которая встречается чаще других.
Медиана Ме = 5,4 показывает, что половина членов ряда не превосходит по величине 5,4.
Задача 5. Двух футболистов, один из которых участвовал в пяти игровых сезонах, а другой – в шести, сравнить по результативности и стабильности в забивании голов, если количество мячей, забитых первым футболистом по сезонам образует ряд: 17,21,20,16,15,19, а вторым: 17,20,18,21,14.
Находим числовые характеристики двух выборок:
Первый футболист: = 18, D(X)
Второй футболист: = 18,D(X)
Таким образом, оба футболиста показывают одинаковую результативность (среднее число голов за сезон), но первый футболист более стабилен, так как дисперсия первой выборки меньше.
ЗАДАНИЕ:
1. ОТВЕТЬТЕ НА ВОПРОСЫ:
2. РЕШИТЕ ЗАДАЧИ 6, 7.
1)да 2)нет 3) да 4)да 5)нет 6)да 7)да 8)да
Задача 7.
Европа-65, Африка-17, Азия-61, Северная и Центральная Америка-16, Южная Америка-15, Австралия-3, все континенты-34
«В среднем в день ребёнок улыбается 400 раз, взрослый — 17. Теперь все улыбнулись, чтобы испортить статистику»
УРОК №81-82
27.12.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «РЕШЕНИЕ ЗАДАЧ. СЛОЖЕНИЕ И УМНОЖЕНИЕ СОБЫТИЙ»
Начнем с задачи.
Предположим, что вероятность получения вами пятерки за контрольную равна 0,5, а четверки – 0,3. Какова вероятность того, что за контрольную вы получите 4 или 5?
Некоторые сразу выпалят: «0,8», но почему именно так? Почему, например, не 0,15 (перемножили, а не сложили)? Разберемся.
Предположим, есть некоторый опыт, у которого есть n исходов. Из них наступлению события A благоприятны k1, а событию B – k2
соответственно
Тогда предположим, что события непересекающиеся, то есть не могут выполняться одновременно. Вот тогда получаем, что благоприятных исходов для объединения – k1 +k2
Значит, вероятность объединения будет равна:
Вероятность объединения несовместных событий равна сумме их вероятностей.
Обратим внимание: здесь речь идет об ОДНОМ эксперименте, в результате которого может наступить либо первое событие, либо второе, но не оба сразу.
В частности, в примере с контрольной мы понимаем, что ученик не может одновременно получить за контрольную и 5, и 4 (речь идет об одной оценке за одну и ту же контрольную), значит, вероятность того, что он получит 4 или 5, равна сумме вероятностей, то есть, все-таки, 0,8.
Ответ: 0,8.
А что делать, если события пересекаются, то есть существуют исходы, благоприятные для них обоих? Такая ситуация будет рассмотрена в конце урока.
Еще один пример.
По статистике футбольный клуб «Вымпел» побеждает в очередном матче с вероятностью 0,2, играет вничью с вероятностью 0,5 и проигрывает с вероятностью 0,3. Какова вероятность того, что «Вымпел» не проиграет следующий матч, если верить статистике?
В данном случае задачу можно решить двумя способами.
Можно применить нашу формулу, ведь если он не проиграет, то он либо сыграет вничью, либо выиграет. Значит, вероятность этого равна 0,7.

Как видите, ответы совпали.
Ответ: 0,7.
Произведение вероятностей
Предположим, что мы провели два разных опыта. Например, ученик написал два экзамена, и каждый из них он сдал на 5 с вероятностью 0,8. Какова вероятность того, что он сдал на 5 оба экзамена?
По аналогии некоторые из вас готовы к 0,8 прибавить 0,8 – это будет 1,6. Многовато для вероятности. Впрочем, если присмотреться, здесь совсем другая ситуация!
Если раньше мы имели дело с двумя непересекающимися событиями для одного эксперимента, то сейчас речь идет об исходах двух экспериментов. А кроме того, раньше мы говорили об объединении (то или то), а сейчас – о пересечении (и то, и то).
Пусть есть первый эксперимент, у него есть
исходов,
благоприятствуют первому событию, а кроме этого, есть второй эксперимент, у него есть n2
Значит, вероятность того, что оба события произойдут, равна
Но это же равно произведению вероятностей наступления каждого из событий:

Мы предположили, что знаем, что благоприятных исходов в первом и втором случаях –
Итак, мы доказали, что вероятность пересечения двух независимых событий равна произведению их вероятностей.
Разберем приведенный выше пример. Если вероятность сдать каждый экзамен равна 0,8 и если допустить, что экзамены сдаются независимо, имеем, что вероятность сдачи обоих равна 0,64. Повторимся: это верно только в том случае, когда мы считаем, что оценки за экзамены получаются независимо друг от друга.
Предположим, что мы дважды подбросили монетку. Какова вероятность того, что оба раза выпадет орел?
Дано:
Найти:
Решение:
Предполагается, что монетка нормальная, то есть вероятность орла и решки – по 0,5. Но тогда вероятность двух орлов будет 0,25, так как события – независимые.
Это работает и для нескольких опытов, не только для двух. Например, вероятность трех орлов подряд будет 0,125, а вероятность ста орлов –
Это иногда называется принципом суперпозиции.
Ответ: 0,25.
Аналогичный принцип суперпозиции верен и для непересекающихся исходов в случае одного эксперимента:
Если вероятность получения тройки – 0,2, четверки – 0,2, пятерки – 0,1, то вероятность получить хотя бы тройку будет равна:
Вы еще не поняли, как же отличить, когда вероятности складывать, а когда перемножать? Очень просто! Если речь идет о двух итогах одного опыта – складываем. А если о двух разных опытах – перемножаем!
Пересекающиеся события
Предположим, что есть события n1 и n2
Это можно проиллюстрировать диаграммой, так называемой диаграммой Эйлера-Венна (см. Рис. 1).
Рис. 1. Пересечение событий
Если объединить те исходы, которые благоприятствуют А1 и те, которые благоприятствуют В1, мы дважды посчитаем те исходы, которые благоприятствуют А и В
То же самое и с вероятностями, ведь к вероятностям мы переходим обычным делением на общее количество исходов.
Получаем формулу:
Например, посчитаем вероятность того, что случайно выбранное трехзначное число делится на 3 либо на 5. Всего чисел – 900. Чисел, делящихся на 3, – 300 (900 : 3)Решение:
А = (трёхзначное число : 3)
В = (трёхзначное число : 5)
Значит,
Домашнее задание
1. Два стрелка стреляют по мишени. Первый стрелок поражает мишень с вероятностью 0,9. Второй стрелок поражает мишень с вероятностью 0,8. Найти вероятность того, что мишень будет поражена.
2. Случайный эксперимент состоит в подбрасывании двух игральных костей. Одна из игральных костей окрашена в синий цвет, другая – в красный. Найти вероятность того, что на синей игральной кости выпадет число 3, а на красной игральной кости выпадет число
УРОК № 79-80
26 .12.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «Сложение и умножение
событий»
События являются несовместными, или несовместимыми, если появление одного из них исключает появление другого.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т. е. P(A+B)=P(A)+P(B).
Пример:
в ящике находятся 9 шаров, среди них 2 белых, 3 красных и 4 зелёных. Наугад берётся один шар. Найди вероятность того, что вынули красный или зелёный шар.
1способ. Пусть событие A — появление красного шара, событие B — появление зелёного шара, тогда событие (A+B) — появление цветного шара. Очевидно, что P(A)= 3 /9 = 1/3 ; P(B)= 4/9
Так как события A и B несовместны, к ним применима теорема сложения вероятностей: P(A+B)=P(A)+P(B)= 1/3 +4/9 =7/9
Ответ: 7/9
Следствие. Сумма вероятностей противоположных событий равна единице, т. е.
P(A)+P(A¯)=1.
Теорема
Для нахождения вероятности противоположного события следует из единицы вычесть вероятность самого события: P(A) = 1-P(A).
Пример:
в ящике находятся 9 шаров, среди них 2 белых, 3 красных и 4 зелёных. Наугад берётся один шар. Найди вероятность того, что вынули красный или зелёный шар.
2 способ. Пусть событие C состоит в том, что вынули белый шар. Тогда противоположное ему событие C¯ состоит в том, что вынули не белый шар, то есть красный или зелёный. Очевидно, что P(C)= 2/9, а согласно следствию из теоремы имеем P(C¯)=1−P(C)=1− 2/9 = 7/9
Ответ: 7/9
Умножение вероятностей
Два события (A) и (B) называют независимыми, если вероятность каждого из них не зависит от появления или не появления другого события.
Если события A и B независимы, то вероятность их одновременного наступления равна произведению вероятностей событий A и B
.Пример:
в случайном эксперименте симметричную монету бросают дважды. Какова вероятность того, что решка выпадет оба раза?
Решение. Результат второй монеты не зависит от результата первой монеты и наоборот, поэтому события являются независимыми. Выпадение решки при одном подбрасывании монеты равно 1/2 , при втором подбрасывании — тоже 1/2. Вероятность того, что решка выпадет два раза, равна 1/2 1/2 = 1/4
Ответ: 1/4
2. Запишите правила сложения и умножения вероятностей.
УРОК №77-78
23.12.2022г. МАТЕМАТИКА. Группа 303. Тема « СОБЫТИЯ. ВЕРОЯТНОСТЬ СОБЫТИЙ»
. В повседневной жизни, в практической и научной деятельности мы часто наблюдаем те или иные явления, проводим определенные эксперименты.
Событие, которое может произойти, а может не произойти в процессе наблюдения или эксперимента, называют случайным событием. Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей.
Прозвенел звонок, выпал снег, черный кот перебежал дорогу – все это события. Каждое из них при одних условиях могло произойти, при других – нет. Поэтому, эти события называют случайными.
Приведите примеры случайных событий.
Приведите примеры маловероятных событий, очень вероятных, достоверных событий, невозможных.
Какие из приведенных событий являются достоверными, а какие невозможными:
а) крокодил научился петь;
б) индюки полетят в теплые края;
в) после марта наступит апрель;
г) завтра наступит суббота;
д) в следующем году твой день рождения придется на среду;
е) брошенный тобой камень долетит до стратосферы?
![]() Два события, которые в данных условиях могут происходить одновременно, называются совместными, а те, которые не могут происходить одновременно, - несовместными.
Два события, которые в данных условиях могут происходить одновременно, называются совместными, а те, которые не могут происходить одновременно, - несовместными.
Примеры 1.
Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» - несовместные.
Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместные.
Ваши примеры..
Равновозможными называются события, когда в их наступлении нет преимуществ.
Не равновозможные события те, у которых в наступлении одного из событий есть какое-то преимущество.
Примеры 2.
Появление герба или надписи при бросании монеты представляют собой равновероятные события.
Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
Ваши примеры.
Событие, которое происходит всегда, называют достоверным.
Вероятность достоверного события равна 1.
Событие, которое не может произойти, называется невозможным.
Вероятность невозможного события равна 0.
Примеры 3.
В следующем году снег не выпадет. При бросании кубика выпадет семерка. Это невозможные события.
В следующем году снег выпадет. При бросании кубика выпадет число, меньше семи. Ежедневный восход солнца. Это достоверные события.
Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара – достоверное событие; появление белого шара – невозможное событие.
Приведите примеры достоверных и невозможных событий.
Занимательная пятиминутка.
Если монету, например рубль, подбросить вверх и позволить ей упасть на пол, то возможны только два исхода: «монета упала гербом вверх» и «монета упала решкой вверх». Случай, когда монета падает на ребро, подкатывается к стене и упирается в нее, бывает очень редко и обычно не рассматривается.
Издавна в России играли в «орлянку» – подбрасывали монету, если надо было решить спорную проблему, у которой не было очевидно справедливого решения, или разыгрывали какой-нибудь приз. В этих ситуациях прибегали к случаю: одни загадывали выпадение «орла», другие – «решки».
К подбрасыванию монеты иногда прибегают даже при решении весьма важных вопросов.
Например, полуфинальный матч на первенство Европы в 1968 году между командами СССР и Италии закончился вничью. Не выявился победитель ни в дополнительное время, ни в серии пенальти. Тогда было решено, что победителя определит его величество случай. Бросили монету. Случай был благосклонен к итальянцам.
ЗАДАНИЕ:
1. Решите задачи
1.Каким (достоверным, невозможным или случайным) является событие:
- Изъятая из колоды одна карта оказалась дамой пик;
- При комнатной температуре и нормальном атмосферном давлении вода оказалась в парообразном состоянии;
- Наугад названное натуральное число оказалось меньше нуля;
- При температуре +20 0 С и нормальном давлении золото оказалось в жидком состоянии.
- В результате броска игрального кубика появилось число 8?
2.Перечислите все элементарные события (равновозможные, не равновозможные, несовместные), которые могут произойти в результате следующего испытания:
Бросается на стол игральный кубик и определяется число очков, появившееся на верхней грани;
Бросается монета и определяется видимая сторона;
Из всех карт одной масти случайным образом выбирается одна карта и определяется изображение на ней;
На пол роняют усечённый конус, выточенный из дерева, и определяют геометрическую фигуру, по которой упавший конус касается пола;
На поверхность стола бросается игральный тетраэдр (грани которого пронумерованы числами 1,2,3,4) и определяется число на той грани, которая лежит на поверхности стола.
2.Запишите конспект сообщения, выделив определения.
УРОК №74-75
21.12.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА, «РЕШЕНИЕ УРАВНЕНИЙ».
Уравнение – это два выражения, соединенные между собой знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестными. Решить уравнений – значит найти все значения неизвестных, при которых оно обращается в верное равенство, или установить, что таких значений нет. Уравнение – одно из важнейших– понятий математики. Обычный путь решения уравнения состоит в том, что с помощью преобразований его сводят к более простым уравнениям, которые называются равносильными. Но при этом нужно быть очень осторожным, потому что при “избавлении от лишнего” можно допустить ошибки.
Поэтому, чтобы не допустить подобных ошибок, сегодня на уроке будем повторять, обобщать, приводить в систему изученные ранее виды, методы и приемы решения рациональных уравнений.
Решите уравнения.
1) 7х5 + 3х4 = 0;
2) х4 + 3х2 – 4 = 0;
3) х3 + х2 + х + 1 = 0;
4) 16х3 – 32х2 – х + 2 = 0;
5) х4 + 6х2 – 27 = 0;
6)  ;
;
7) (х2 – 5)2 + 2(х2 – 5)2 + 1 = 0;
8) (х2 – 2х) (х2 + 4 – 2х) = 3.
9) (х2 + х + 6) (х2 + х – 4) = 144.
10)  = 3.
= 3.
Оценивание домашней работы проводится в форме самооценки. В тетради выставляется:
- оценка “5” – решено 8 и более уравнений;
- оценка “4”-решено 6-7 уравнений;
- оценка “3”– решено 3-5 уравнений.
Тест (В течение 8 минут осуществляется проверка навыков решения простейших уравнений)
№ п/п | Вариант 1 | Ответы | Вариант 2 | Ответы |
1 | (х-10)(х+2)=0 | 10; -2 | (х-5)(х+9) | 5; -9 |
2 | х2 + 3х – 54 = 0 | 6;-9 | х2-4х+3=0 | 1;3 |
3 | х2-81=0 | 9;-9 | х2-49=0 | 7;-7 |
4 | х/6=0 | 0 | х/8=0 | 0 |
5 | (х-8)/9=0 | 8 | (х-12)/15=0 | 12 |
6 | (х+3)/х=0 | -3 | (х+8)/2=0 | -8 |
7 | (36– х2)(х-5)=0 | 6;-6;5 | (х+3)( х2-25)=0 | -3;5;-5 |
8 | 0/5х=0 | х– любое число | 0/х=5 | нет решений |
9 | х2+3х+4=0 | нет решений | х2+5х+7=0 | нет решений |
10 | (х2-25)/(х-5)=0 | -5 | (х2-4)/(х+2)=0 | 2 |
. Оценивание осуществляется при помощи взаимопроверки.
- оценка “5” – решено 10 уравнений;
- оценка “4” – решено 8–9 уравнений;
- оценка “3”– решено 5–7 уравнений;
- оценка “2”– решено менее 4 уравнений.
Случаи решения рациональных уравнений
Целым рациональным уравнением степени n стандартного вида называется уравнение вида:
an xn+ an-1xn-1+…+ a1x+ an =0
Любое целое уравнение с помощью формул можно привести к стандартному виду. Всякое целое уравнение степени n имеет не более n корней.
Частные случаи рационального уравнения.
1. Если n=1, то уравнения вида ах+в=0 являются линейными:
– если а=0, то уравнение имеет единственное решение х=-в/а;
– если а=0, в не равно 0, то уравнение не имеет корней;
– если а=в=0, то уравнение имеет бесконечно много корней.
2.если n=2, то получаем квадратное уравнение ах2+вх +с=0. Оно может быть полным (если все коэффициенты отличны от нуля) или неполным(если хотя бы один коэффициент не равен нулю).
Неполные:
а) в=0, с=0
ах+с=0
х=-с/а
б) в=с=0
ах=0
х=0
в) с=0
ах2+вх=0
х(ах+в)=0
х=0, х=-в/а
Полные:
ах2+вх+с=0
D=в2-4ас
Если D>0, то х1=(-в+VD)/2a х2=(-в-VD)/2a
Если D<0, корней нет.
Если D=0,то х=-в/2а
По теореме Виета, если х2+х +с=0 имеет корни х1 и х2, то х1 + х2= -в/2а, х1 х2=с/а.
Частный случай теоремы Виета.
Если сумма коэффициентов приведенного квадратного уравнения равна нулю, т. е.1+p+q=0, то х1=1,х2=q.
Пример х+2х+q=0,то х=1, х=q
Т.к. 1+2+3=0, значит х=1,х=3.
3. Если n>2, то решение общего вида рационального уравнения представляет некоторые трудности. Для решения уравнений третьей и четвертой степени существует формулы вычислений корней. Но эти формулы сложные в применении и ими почти не пользуются. Для уравнений пятой степени и выше общих формул вообще не существует. Поэтому в математике разработаны различные методы, позволяющие находить с любой точностью приближенные значения корней. Также существует два основных аналитических метода, позволяющих найти точное значение корней рационального уравнения.
1 способ. Метод разложения на множители.
Принцип решения уравнений таким методом– разложение на множители его левой части (произведение равно нулю, если хотя бы один множитель равен нулю, а остальные при этом определены).
Способы разложения на множители:
- вынесение общего множителя за скобки;
- применение формул сокращенного умножения;
- группировка слагаемых:
- применение формулы разложения квадратного трехчлена на множители.
Нередко в таких заданиях теорема Безу, позволяющая находить целые корни уравнения: если целое рациональное уравнение с целыми коэффициентами имеет целые корни, то они являются делителями свободного члена.
2 способ. Метод введения новой переменной.
Этот метод используется при решении уравнения вида ах4+вх2+с=0, которое называется биквадратным. Для нахождения корней этого уравнения производится замена х=у.
Этот способ можно использовать при решении очень многих уравнений.
Например:
(х+1)(х+2)(х+3)(х+4)=24
Группируем первый множитель с последним, второй с третьим.
Получаем (х+5х+4)(х+5х+6)=24 заменяем х+5х=у и получаем уравнение
(у+4)(у+6)-24=0 | |
у=0 | у=10 |
Ответ: 0; -5
Этот прием можно обобщить для уравнения вида (х+а)(х+в)(х+с)(х+п)=А, если а+с=в+п или присутствует равенство сумм каких либо других пар этих чисел.
Но бывает и так, что трудно угадать, какую новую переменную нужно ввести, чтобы упростить уравнение. Поэтому нужно рассматривать различные виды целых рациональных уравнений, для упрощения которых известна подстановка. Например, возвратные уравнения ( Уравнение четвертой степени называется возвратным, если оно имеет вид ax4+ вx3+ сx2 + вx + a =0, т.е. симметричные коэффициенты одинаковы.
Это уравнение решается подстановкой у=х+1/х
Например.
х4-7x3+ 14x2-7х + 1 =0, х2 не является корнем уравнения, значит можно разделить обе части уравнения на х:
х2-7х+14-7/х+1/х2=0
группируем равноотстоящие от концов слагаемые (х2+1/ х2)-7(х+1)+14=0, решая данное уравнение получаем четыре корня.
3 способ.
Графический метод
Данный метод применим для решения очень многих уравнений. Его суть состоит в том, что уравнение сводится к виду q(x)=f(x), где q и f функции, графики которых известны. Например, уравнение х3-х+3=0 может быть решено графически, если его переписать в виде х3=х+3 и построить графики функций у= х3 и у=х+3.
ЗАДАНИЕ:
1. Составьте конспект сообщения.
2. Решить уравнения
1) х4+х2 -6=0
2) ( х2+х -1)( х2+х +1)=2
3) х(х+1)(х+2)(х+3)=-3/4
4) х3-х2 -9х-6=0
5) х4-5х3 +6х2 -5х+1=0
УРОК № 70-71
19.12.2022г. Группа 303. МАТЕМАТИКА. ТЕМА. «Бином Ньютона. Свойства биноминальных коэффициентов»
На прошлом уроке мы познакомились с основами комбинаторики. Какие же ученые внесли вклад в развитие комбинаторики как науки? Одним из выдающихся умов того времени был английский ученый Исаак Ньютон.
Бином Ньютона. .Слово бином означает «Два числа». В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять. Вы, наверняка, помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных ра
(a + b)4 = (a + b)(a + b)3 = (a + b) (a3 + 3a2b + 3ab2 + b3)= a4 +4a3b + 6a2b2 + 4ab3 + b4
Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:
Возможно, вы уже догадались, что «рояль в кустах» – это треугольник Паскаля на предыдущей странице. Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двухстрок, легко сделать полным (получить строчки при
Окончательно получим:
Это утверждение было известно задолго до Паскаля - его знал живший в XI-XII вв. среднеазиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло). Первое, дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ал-Туси, где дана таблица чисел (биномиальных коэффициентов).
Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г..
Теперь понятно, как возвести бином в любую степень n. В левой части записываем (а+b)n. А в правой части записываем сумму аn + an-1b+ … + bn , оставляя в каждом слагаемом место для коэффициента. И эти места заполняем числами из n–ой строчки треугольника Паскаля, которую, конечно, нужно заранее выписать.
Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:
.(a +b)m = C0m am + C1m am-1b + C2m am-2 b2 + … Cnm am-n bn + … + Cmm-1 abm-1 + Cmm bm
Данную формулу называют биномом Ньютона, а числа Сmn – биномиальными коэффициентами, которые могут быть найдены по формуле
Сmn = m!/(m-n)! n!
Пример:
(a + b)5 = a5 + C15 a4 b + C25 a3b2 + C35 a2 b3 + C45 ab4 + C55 b5 = a5 + 5a4 b+ 10 + 10a2 b3 + 5ab4 + b5
Таким образом можно записать формулу для возведения двучлена в любую степень. Давайте заметим некоторые свойства у слагаемых в разложении двучлена по формуле Бинома Ньютона.
Свойства бинома Ньютона
1) Число слагаемых на 1 больше степени бинома.
2) Коэффициенты находятся по треугольнику Паскаля или равны числу сочетаний Сnm, где n – степень двучлена , m – переменная величина, пробегающая значения от 0 до n и соответствующая степени второго выражения.
3) Коэффициенты симметричны.
4) Если в скобке знак минус, то знаки + и – чередуются.
5) Сумма степеней каждого слагаемого равна степени бинома.
6) Сумма коэффициентов разложения ( a + b)n равна 2n .
Мы знакомились с вами с применением бинома Ньютона при изучении формул сокращенного умножения.
ЗАДАНИЕ:
1. Внимательно прочтите сообщение. Выпишите определение Бинома и формулу бинома Ньютона.
2. Выпишите свойства бинома Ньютона
3. Записать разложение бинома:
А) (1 +х)8; б) (3х +2)4; в) (3х – 1/3)5
енных мальчика должны войти в команду?
УРОК №66-67
16.12.2022г. ГРУППА 303.Тема: «Задачи на подсчет числа размещений, перестановок, сочетаний».
Решение задач:
№1. Экзамен состоит из 5 задач, которые можно решать в любом порядке. Сколькими способами можно расставить задачи. (
№2. В магазине продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора. (
1. Перестановка
Рассмотрим слово «КВАНТ», состоящее из 5 различных букв. Если менять порядок букв, получим 5!=120 перестановок
Если проделать то же самое со словом «АТАКА», то перестановок будет меньше, потому что, меняя местами 1,3 и 5-ю буквы, будем получать то же самое слово. Т.к. три буквы А можно менять местами 3!=6 способами, то перестановок будет в слове «АТАКА» в 6 раз меньше, т.е. 20
Вывод: Перестановками в такой выборке, где есть один элемент, называются перестановками с повторениями. Обозначается : Р(n1, n2,….., nk)
Р(n1, n2,….., nk ) = 
Задача: Сколько различных перестановок можно сделать из букв слова «МАТЕМАТИКА»
Решение:
Всего – 10 букв
«М» - 2 повтора
«А» - 3 повтора
«Т» - 2 повтора
«Е» - 1 повтор
«И» - 1 повтор
«К»- 1 повтор
Ответ: 151200 перестановки
2. Сочетания.
Рассмотрим следующую задачу.
В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить 8 различных открыток?
Решение. Данная задача на отыскание числа сочетаний без повторений, т.к. требуется купить 8 различных открыток
Ответ: 45 способов
Проделаем то же самое, но только определим «Сколькими способами можно купить в нем 8 открыток?
Решение.
Данная задача на отыскание числа сочетаний с повторениями из n = 10 элементов по k =8. Следовательно, она решается по формуле
Вывод: Иными словами, выборки которые отличаются количеством элементов хотя бы одного типа, называются сочетаниями с повторениями, а их общее число будем обозначать
Задача: В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?Решение. В задаче требуется найти число всевозможных групп по 9 элементов, которые можно составить из данных трех различных элементов, причем указанные элементы в каждой группе могут повторяться, а сами группы отличаются друг от друга хотя бы одним элементом. Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,
3. Размещения.
Рассмотрим задачу:
В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими различными способами могут выйти пассажиры на каждом этаже, начиная со второго?
А теперь ту же задачу, но вопрос сформулируем иначе.
В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?
Задача такого вида называется «размещения с повторением», обозначается
и вычисляется по принципу умножения. Вычисляется по следующей формуле:
Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:
Задача: Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, ЕСли каждый ящик может вместить все куклы?
Ответ: 312
.Задача №1. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
Решение. Число всех букв, каждая из которых записывается одним символом, равно
Число всех букв, каждая из которых записывается двумя символами, равно
Число всех букв, каждая из которых записывается тремя символами, равно Число всех букв, каждая из которых записывается четырьмя символами, равно Число всех букв, каждая из которых записывается пятью символами, равно Число всех указанных букв будет равно 62.Задача №2. Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае. Поскольку
ЗАДАНИЕ:
1. Выпишите формулы нахождения: перестановок, размещения, соединения с повторениями и без.
2 Решите задачи:
1. Сколькими способами можно разместить 8 пассажиров по трем вагонам?
2. Сколькими способами Буратино, кот Базилио и лиса Алиса могут поделить между собой 5 одинаковых золотых монет?
Ответ:
3. Сколько различных браслетов можно сделать из 5 одинаковых изумрудов, 6 одинаковых рубинов и 7 одинаковых сапфиров ( всего в браслет входит 18 камней)?
14.12.2022г. ГРУППА 303. МАТЕМАТИКА ТЕМА «Комбинаторика - основные понятия и формулы. Перестановки, размещения, сочетания. Основные понятия и формулы»
Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Общее число N способов, которыми можно выбрать по одному элементу из каждой группы и расставить их в определенном порядке (то есть получить упорядоченную совокупность ( a b c d), равно:
N = n1 ∙ n2 ∙… nn
Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?
Решение
Первая монета имеет n1 = 2 альтернативы – либо орел, либо решка. Для второй монеты также есть n2 = 2 альтернативы и т.д., т.е. n1 = n2 =n3 =23 =8
Искомое количество способов:
N =n1 +n2 + …nn
Правило сложения
Если любые две группы A1 и A2 не имеют общих элементов, то выбор одного элемента или из A1 , или из A2…или из Ak можно осуществить способами.
N = n1 +n2 + …nk
Пример 2
На полке 30 книг, из них 20 математических, 6 технических и 4 экономических. Сколько существует способов выбора одной математической или одной экономической книги.
Решение
Математическая книга может быть выбрана n1 =20 способами, экономическая – n2 =4 способами.
По правилу суммы существует N способа выбора математической или экономической книги. N = n1 +n2 =20 + 4 =24
Размещения и перестановки
Размещения – это упорядоченные совокупности элементов, отличающиеся друг от друга либо составом, либо порядком элементов.
Размещения без повторений, когда отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется последовательным выбором без возвращения, а его результат – размещением без повторений из n элементов по k .
Число различных способов, которыми можно произвести последовательный выбор без возвращения элементов из генеральной совокупности объема , равно:
Расписание дня состоит из 5 различных уроков. Определите число вариантов расписания при выборе из 11 дисциплин.
Решение
Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и порядком следования. поэтому:
Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из n элементов равно
Пример 4
Сколькими способами можно рассадить 4 человек за одним столом?
Решение
Каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
Размещения с повторениями, когда отобранный элемент перед отбором следующего возвращается в генеральную совокупность. Такой выбор называется последовательным выбором с возвращением, а его результат - размещением с повторениями из n элементов по k.
Общее число различных способов, которыми можно произвести выбор с возвращением k элементов из генеральной совокупности объема n, равно
An-k = nk
Пример 5
Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?
Решение
Каждый из способов распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком. Так как одном этаже может выйти как один, так и несколько пассажиров, то одни и те же пассажиры могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 7 элементов по 6:
Сочетания
Сочетаниями из Cn элементов по k называются неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним элементом.
Пусть из генеральной совокупности берется сразу несколько элементов (либо элементы берут последовательно, но порядок их появления не учитывается). В результате такого одновременного неупорядоченного выбора n элементов из генеральной совокупности объема k получаются комбинации, которые называются сочетаниями без повторений из n элементов по k .
Число сочетаний из n элементов по k равно: Cnk = ![]()
Пример 6
В ящике 9 яблок. Сколькими способами можно выбрать 3 яблока из ящика?
Решение
Каждый вариант выбора состоит из 3 яблок и отличается от других только составом, то есть представляет собой сочетания без повторений из 9 элементов:
Количество способов, которыми можно выбрать 3 яблока из 9:
Пусть из генеральной совокупности объема выбирается элементов, один за другим, причем каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность. При этом ведется запись, какие элементы появились и сколько раз, однако порядок их появления не учитывается. Получившиеся совокупности называются сочетаниями с повторениями из n элементов по k. Число сочетаний с повторениями из n элементов по k:
Cn-k = Ck n+k-1
На почте продают открытки 3 видов. Сколькими способами можно купить 6 открыток?
Решение
Это задача на отыскание числа сочетаний с повторениями из 3 по 6
N = C3-6 = C 63 +6 -1 =C86 =![]() =
= ![]() =28
=28
Разбиение множества на групп
Пусть множество из различных элементов разбивается на k групп так, то в первую группу попадают n1 элементов, во вторую n2- элементов, в k-ю группу – nk элементов, причем n1+n2+…nk =n
Такую ситуацию называют разбиением множества на k группы.
Число разбиений на групп, когда в первую попадают элементов, во вторую - элементов, в k-ю группу - элементов, равно: N (n1 n2 ... nk) =![]()
Пример 8
Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?
Решение
Здесь n =16 k =3 n1 =5 n2 = 7 n3 =4
Число разбиений на 3 подгруппы:
ВЫВОД
1. Сделайте конспект сообщения, выписав определения и формулы.
2.Решите задачу: Какими способами можно рассадить 6 человек за одним столом?
УРОК № 63
13 .12.2022г. ГРУППА 303. МАТЕМАТИКА. КОНТРОЛЬНАЯ РАБОТА №4
ВАРИАНТ 1
1. Найдите площадь полной поверхности и объем тела, полученного при вращении прямоугольника со сторонами 6 см и 10 см вокруг его оси симметрии, параллельной большей стороне.
2. Найдите площадь полной поверхности и объем тела, полученного при вращении прямоугольного треугольника с катетом 6 см и гипотенузой 10 см вокруг его катета.
3. Найдите объем шара и площадь его поверхности, если его радиус – 4 см.
4. Написать уравнение сферы радиуса 3 дм с центром в точке А (-2;-3;5)
5. Радиусы двух шаров – 5 мм и 4 мм. Определите радиус шара, объем которого равен суммарному объему данных шаров.
ВАРИАНТ 2
1. Найдите площадь полной поверхности и объем тела, полученного при вращении прямоугольника со сторонами 4 см и 8 см вокруг его оси симметрии, параллельной большей стороне.
2. Найдите площадь полной поверхности и объем тела, полученного при вращении прямоугольного треугольника с катетом 4 см и гипотенузой 5 см вокруг его катета.
3. Найдите объем шара и площадь его поверхности, если его радиус – 5 см.
4. Написать уравнение сферы радиуса 3 дм с центром в точке А (-1;-2; 4).
5. Радиусы двух шаров – 3 мм и 4 мм. Определите радиус шара, объем которого равен данных шаров суммарному объему.
Для того, чтобы выполнить эту контрольную работу, необходимо повторить предыдущую тему «Измерения в геометрии. Решение задач», в которой даны все формулы вычисления площадей поверхностей геометрических тел и их объёмов.
Выберите один вариант. Все задачи сопровождаются рисунками.
ЖЕЛАЮ УСПЕХА!
УРОК № 61-62
12.12.2022г. ГРУППА 303.МАТЕМАТИКА «ИЗМЕРЕНИЯ В ГЕОМЕТРИИ»
На этом уроке мы с вами вспомним изученный ранее материал на уроках геометрии, о значении его для изучения и в практической деятельности.
Объем — это одна из характеристик трехмерных геометрических фигур.
Объем обозначается большой латинской буквой V («вэ»). Величины объема взаимосвязаны (одну кубическую единицу объема можно заменить другой).
Правило. Объем прямоугольного параллелепипеда равен произведению трех его измерений. V = abc
Единицами измерения объема служат:
а) стандартные единицы длины в кубе:
1 см3 = 1 000 мм3
1 дм3 = 1 000 см3 = 1 000 000 мм3
1 м3 = 1 000 дм3 = 1 000 000 см3= 1 000 000 000 мм3
1 км3=1 000 000 000 м3
б) специальная единица объема (литр):
1 л = 1 дм3 = 1 000 см3.
В качестве единицы измерения выбирают кубик с ребром, равным какой-нибудь единице длины, например 1 см. Тогда единицей измерения объема будет объем такого кубика .
Например, объем прямоугольного параллелепипеда (рис. 65) равен 24 см3. Это значит, что его объем содержит 24 кубика объемом по 1 см3. Этот же результат можно получить, если измерить длину a, ширину b и высоту c тела, а затем их значения перемножить.
В СИ единицей объема является 1 м3.
Другие единицы: дм3, см3, мм3— дольные единицы м3.
1м3 =1000дм3 =1•103 дм3;
1дм3 =1000см3 =1•103 см3;
1см3 =1000мм3 =1•10 3 мм3;
1дм3 =0,001м3 =1•10-3 м3;
1см3 =0,001дм3 =0,000001м3 =1•10-6 м3;
1мм3 =0,001см3 =1•10-3 см3;
1мм3 =0,000001дм3 =1•10-6 дм3;
1 мм3 = 0,000000001м3 = 1 • 10-9 м3
Изучение стереометрии начинается со знания формул. Для решения задач по стереометрии на нахождение объемов и площадей поверхностей многогранников и тел вращения в основном нужны: формулы объёмов, формулы площадей поверхностей, формулы площадей плоскостных фигур и
элементарная логика.
Многогранники.
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Тела вращения
Цилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения.
Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси.
Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует.
В нашем курсе математики рассматриваются только прямые цилиндры и конусы.
Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.
Развертки цилиндра и конуса
Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры.
Площади боковой поверхности цилиндра и конуса
Правило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра.
Sб. = C H = 2πR H
где C — длина окружности, H — высота цилиндра, R — радиус окружности основания.
Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.
Sб = ![]() C l =
C l = ![]() 2πR l =πRl
2πR l =πRl
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.
Площадь поверхности шара
Правило. Площадь поверхности шара равна учетверенной площади большого круга шара.
Sш. = 4 πR2
где R — радиус шара
Объемы цилиндра, конуса и шара
Правило. Объем цилиндра равен произведению площади основания высоты.
V = Sосн. H = πR2 H
где R — радиус основания, H — высота цилиндра.
Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса.
V = ![]() Sосн. H =
Sосн. H = ![]() π R2 H
π R2 H
где R — радиус основания, H — высота конуса.
Правило. Объем шара равен четырем третям
произведения числа Пи на куб радиуса.
V =![]() π R3
π R3
где R — радиус шара
Цилиндр
Площадь боковой поверхности:
Sб = 2πRH
Площадь полной поверхности:
Sполн. = Sб + 2Sосн. = 2πRH + 2πR2
Объем:
V = Sосн. H = πR2 H
Конус
Площадь боковой поверхности:
Sб = πRl
Площадь полной поверхности:
S = S + S = πRl + πR2
Объем:
V =![]() S H =
S H = ![]() πR2H
πR2H
Усеченный конус Шар
S = π (r + r1)l
V = ![]() H (S + S1 +
H (S + S1 + ![]() ) V =
) V =![]() π R3
π R3
Подобие тел
Подобные тела. Зеркально подобные тела и фигуры.
Два тела подобны, если одно из них может быть получено из другого путём увеличения (или уменьшения ) всех его линейных размеров в одном и том же отношении. Автомобиль и его модель – подобные тела.
Два тела (фигуры) зеркально подобны, если одно из них подобно зеркальному отражению другого. Например, картина и её фотонегатив зеркально подобны друг другу.
В подобных и зеркально подобных фигурах все соответственные углы (линейные и двугранные) равны.
В подобных телах многогранные и телесные углы равны; в зеркально подобных телах они зеркально равны.
Если два тетраэдра (две треугольные пирамиды) имеют соответственно пропорциональные рёбра ( или соответственно подобные грани ), то они подобны или зеркально подобны. Например, если грани первой пирамиды вдвое больше, чем у второй, то высоты, апофемы, радиус описанного круга первой пирамиды также вдвое больше, чем у второй. Эта теорема не имеет места для многогранников с большим числом граней. Предположим, что мы соединили все рёбра куба в его вершинах посредством шарниров; тогда мы можем изменить форму этой фигуры, не растягивая её стержни, и получить из начального куба параллелепипед.
Две правильные призмы или пирамиды с одинаковым числом граней подобны, если радиусы их оснований пропорциональны их высотам. Два круглых цилиндра или конуса подобны, если радиусы их оснований пропорциональны их высотам.
Если два и более тел подобны, то площади всех соответствующих плоских и кривых поверхностей этих тел пропорциональны квадратам любых соответствующих отрезков.
Если два и более тел подобны, то их объёмы, а также объёмы любых их соответствующих частей, пропорциональны кубам любых соответствующих отрезков.
РЕШЕНИЕ ЗАДАЧ
V = a * b * c
где а — длина, Ь — ширина, с — высота.
Так как у куба все измерения равны (а = Ь = с), то формула для вычисления объема куба V = а3.
Примеры
1.Вычислить объем прямоугольного параллелепипеда длиной 6 м, шириной 4 м и высотой 8 м.
Решение. Так как длина, ширина и высота измеряются одной и той же единицей длины (м), то подставим их в формулу V=а*Ь*с и вычислим объем:
V = 6 * 4 * 8 = 192 (м3)
Ответ: 192 м3.
2.Вычислите объем куба со стороной основания 10 см.
Решение. Подставим численное значение стороны куба в формулу вычисления объема V=а3 и вычислим:
V = 10 * 10 * 10 = 103 = 1 000 (см3) — 1 л.
Ответ: 1 000 см3, или 1 л.
Некоторые задачи по стереометрии решаются вообще без формул!
Например.
3.Объём куба равен 12. Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Обойдёмся без формул!
Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб :-)
Площадь поверхности многогранника — это сумма площадей всех его граней.
4.В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в 27раз.
5.Чашка диаметром 8 см и высотой 10 см вмещает 0.5 литра воды. Каких размеров должна быть подобная чашка, вмещающая 4 литра воды ?
Решение
Поскольку чашки – подобные цилиндры, то отношение их объёмов равно отношению кубов соответствующих отрезков ( в нашем случае – высот и диаметров чашек ). Следовательно, высота h новой чашки находится из отношения: ( h / 10 ) 3 = 4 / 0.5, то есть h 3 = 8 · 10 3, откуда h = 20 см; аналогично, для диаметра d получим: ( d / 8 )3 = 4 / 0.5 , то есть d3 = 8 · 83, откуда d = 16 см . |
Задания для самостоятельной работы
1.В каком отношении делится боковая поверхность правильной треугольной призмы плоскостью, проходящей через среднюю линию ее основания.(2 балла)
2. В прямоугольном параллелепипеде стороны основания 3 и 4, а диагональ наклонена к плоскости основания под углом 45°.Найдите площадь поверхности параллелепипеда.(4 балла)
3. Найдите площадь боковой поверхности прямоугольного параллелепипеда, у которого стороны основания 5 и 6,а боковые ребра 7. (4 балла)
4. В правильной четырехугольной пирамиде сторона основания равна 6. Боковая грань наклонена к плоскости основания под углом 45°. Какова площадь поверхности пирамиды? (4 балла)
5. Можно ли из куска жести прямоугольной формы размером 31х11см сделать открытую сверху коробку, имеющую форму прямоугольного параллелепипеда размером 10х10х6см? (5 баллов)
6. Стороны прямоугольника 4 и 5.Какова площадь поверхности тела , полученного вращением этого прямоугольника вокруг меньшей стороны? (4 балла)
7. Из скольки кубиков, с ребром 3 см каждый можно составить куб ,с ребром 15 см?(2 балла)
8. Каков объем прямоугольного параллелепипеда, у которого ребра основания 6 и 8, а диагональ наклонена к плоскости основания под углом 30°? (3 балла)
Эталоны ответов
1:4
94
147
![]()
Нет
96π
375
160![]()
УРОК №59-60
09.12.2022г. Группа 303. Математика. Тема. «Решение задач . Объёмы тел»
На прошлом уроке мы с вами ввели понятие объёма геометрических тел, записали формулы объёмов. Сегодня мы будем применять полученные знания для решения задач.
Решение задач
Самостоятельное решение:
УСПЕХА ВАМ!
УРОК №55-56
06.12.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «ФОРМУЛЫ ОБЪЁМА ШАРА И ПОВЕРХНОСТИ СФЕРЫ»
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии не больше данного от данной точки.
Поверхность шара называется сферой.
Рис. 1. Вращение полукруга |
|
Рис.2 ШАР
Сечение шара плоскостью, проходящей через центр шара, называется большим кругом.
Для упрощения обычно рисуется не шар, а большой круг шара.
Рис. 3 Большой круг шара | |
Площадь поверхности шара (т. е. сферы) вычисляется по формуле S(сферы)= 4⋅π⋅R2, где R — радиус шара.
РЕШАЕМ ЗАДАЧИ.
РЕШИТЕ САМОСТОЯТЕЛЬНО:
№ 1. Объем шара равен 36π см3. Найти его радиус.
№ 2. Объемы двух шаров относятся как 8 : 1. Найдите отношение их радиусов.
№ 3. В шар вписан куб со стороной а. Найдите объем шара.
УРОК №53-54
05.12.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЁМ КОНУСА»
Площадь поверхности конуса состоит из площади боковой поверхности конуса и площади основания (круга).
Площадью боковой поверхности конуса является площадь её развёртки.
Площадь боковой поверхности конуса вычисляется по формуле: S(бок.)=πRl, где R — радиус конуса, l — образующая конуса. Площадь основания конуса вычисляется по формуле S(круга) =πR2. Площадь полной поверхности конуса вычисляется по формуле S(полн.) =S(бок.) +S(круга) =πRl+πR2. Объём конуса вычисляют по формуле V = |
Развёрткой боковой поверхности конуса является круговой сектор.
S(сектора) =πl2α/3600, где |
l – образующая
ά- градусная мера дуги АКВ
Площадь и объём усечённого конуса
Решите задачи
1. Смолу для промышленных нужд собирают, подвешивая конические воронки к соснам. Сколько воронок диаметром 10 см с образующей 13 см нужно собрать, чтобы заполнить 10-литровое ведро?
2. Цилиндр и конус имеют общее основание и общую высоту. Вычислить объём цилиндра, если объём конуса равен 40.
3. Во сколько раз увеличится боковая поверхность конуса, если его образующую увеличить вдвое, а радиус основания одновременно в 3 раза.
УРОК №51-52
02.12.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «Цилиндр. Площадь поверхности и объём»
Прямым круговым цилиндром называется тело, образованное вращением прямоугольника вокруг его стороны.
На рис. 263 изображен цилиндр, образованный вращением плоского прямоугольника ОАВО1 вокруг прямой ОО1 - оси цилиндра.
Стороны ОА и O1 B описывают равные круги, которые лежат в параллельных плоскостях, называются основаниями цилиндра. Радиусы кругов называются радиусами цилиндра.
Сторона АВ описывает поверхность, которая называется боковой поверхностью цилиндра. Отрезки боковой поверхности, которые параллельны и равны АВ, называются созидательными цилиндра.
Высотой цилиндра называется отрезок, перпендикулярный к основаниям цилиндра, концы которого принадлежат основаниям. Высота цилиндра равна его образующей.
Осевое сечение цилиндра - прямоугольник со сторонами, равными высоте цилиндра и диаметру его основания. На рис. 264 прямоугольник ABCD - осевое сечение цилиндра.
ЗАДАНИЯ
1. 1. Приведите примеры бытовых предметов, которые имеют форму цилиндра.
2. 2. Пользуясь рис. 264, назовите:
а) радиус цилиндра;
б) образующую цилиндра.
1. 3. Какие свойства имеют основания цилиндра?
2. 4. Какие свойства имеют образующие цилиндра?
3. 5. Из кучи картона взяли лист и вырезали круг. Достали цилиндр с очень малой высотой. Как практически определить его высоту?
4. 6. Кусок тонкой проволоки можно считать цилиндром, у которого радиус очень мал. Как практически определить этот радиус?
Площадь поверхности и объем цилиндра
Поверхность цилиндра состоит из двух равных оснований и боковой поверхности.
Если поверхность цилиндра разрезать по окружностям оснований и одной из образующих, а затем развернуть на плоскости, то получим развертку цилиндра (рис. 265). Она состоит из прямоугольника, стороны которого равны длине окружности оснований и высоте цилиндра, и двух кругов, что является основаниями цилиндра.
Площадью боковой и полной поверхности цилиндра называют площадь развертки боковой и полной поверхностей.
Тогда площадь боковой поверхности Sб. и площадь полной поверхности Sп. цилиндра определяются формулами:
Sб. = 2
где R, H - радиус и высота цилиндра соответственно.
Объем цилиндра равен произведению площади его основания на высоту V = Sо. ∙ H.
Если радиус основания цилиндра равен R, а высота Н, то его объём
V =π R2 Н
Решение задач
1. 1. Диаметр цилиндра равен 1 см, а высота равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.
2. 2. Площадь боковой поверхности цилиндра равна 15π см2. Найдите площадь осевого сечения цилиндра.
3. 3. Осевым сечением цилиндра является квадрат со стороной 8 см. Найдите боковую и полную поверхности цилиндра.
4. 4. Найдите объем тела, образованного при вращении прямоугольника вокруг его стороны, которая равна 2 см.
5. 5. Осевое сечение цилиндра - квадрат со стороной 8 см. Найдите объем цилиндра.
6. 6. Найдите объем цилиндра, если развертка его боковой поверхности - квадрат со стороной 8 см.
2.Составьте конспект (образец приведен в табл. 12).
Таблица 12
Цилиндр | |
Прямым круговым цилиндром называется тело, образованное вращением прямоугольника вокруг его стороны. ОА, О1В - радиусы, АВ - образующая (высота), O1O - ось | |
Площадь поверхности цилиндра Sцил = Sбоков + 2Sосн, где Sбоков = 2nRH, Sосн = nR2 | |
Объем цилиндра V = Sосн ∙ H; | |
3. Изучите формулу площади поверхности и объема цилиндра.
1. 1. Дайте определение цилиндра.
2. 2. Что такое высота цилиндра? осевое сечение цилиндра?
3. 3. Чему равна площадь боковой поверхности цилиндра?
4. 4. Чему равен объем цилиндра?
5. 5. На рис. 268 изображен цилиндр, радиус которого равен 3 см, а высота - 4 см. Определите, какие из приведенных утверждений являются правильными, а какие - неправильными.
а) Длина окружности основания цилиндра равна 6ϖ см.
б) Площадь основания цилиндра равна 6ϖ см2 .
в) Площадь боковой поверхности цилиндра равна 2ϖ см2 .
г) Объем цилиндра равен 24ϖ см3.
УРОК №49-50
30.11.2022г. ГРУППА 303 ГЕОМЕТРИЯ. ТЕМА "Пирамида. Площадь поверхности и объём"
Пирамида и ее элементы
n-угольной пирамидой называется многогранник, одна грань которого - произвольный n-угольник, а все остальные п граней - треугольники, имеющие общую вершину.
Общую вершину треугольных граней называют вершиной пирамиды, противоположную ей грань - основанием, а все остальные грани - боковыми гранями пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Перпендикуляр, опущенный из вершины пирамиды на плоскость ее основания, называют высотой пирамиды.
На рис. 253 изображен четырехугольную пирамиду SABCD; точка S - ее вершина, ABCD - основание; SA, SB, SC, SD - боковые ребра; АВ, ВС, CD, AD - ребра основания; SO - высота пирамиды.
Правильную треугольную пирамиду называют также тетраэдром. Сумму площадей всех боковых граней пирамиды называют площадью боковой поверхности пирамиды. Чтобы найти площадь всей поверхности пирамиды, нужно к площади Sбоков ее боковой поверхности прибавить площадь Sосн основания: S = Sб. + Sосн.
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника (рис. 254).
Все боковые ребра правильной пирамиды равны, все боковые грани - равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. На рис. 254 SF
ЗАДАНИЕ:
1. 1. Сколько граней, ребер, вершин имеет n-угольная пирамида?
2. 2. Каждое ребро тетраэдра равен 2 см. Найдите площадь поверхности тетраэдра.
3. 3. Постройте треугольную и четырехугольную пирамиды.
Площадь поверхности и объем пирамиды
Теорема. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра ее основания на апофему.
Доказательство:
Пусть а - сторона основания правильной n-угольной пирамиды (рис. 255). SH
Тогда площадь боковой грани
и правильной пирамиды равна ½ am, а площадь боковой поверхности Sб. = ½ а ∙m ∙n. Так 1/2аn = р, где р - полупериметр основания пирамиды, то Sб. = pm.
Объем любой пирамиды равен трети произведения площади ее основания на высоту: V = 1/3 Sосн ∙ H.
Задачи. 1. Найдите площадь боковой поверхности правильной треугольной пирамиды, если сторона основания равна 12 см, а апофема 10 см.
1. 2. Найдите площадь боковой поверхности правильной четырехугольной пирамиды, если сторона основания равна 16 см, а боковое ребро 10 см.
2. 3. Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 6 см, а высота 10 см.
Составьтет конспект (образец приведен в табл. 11).
Таблица 11
Пирамида | |
n-угольная пирамида - многогранник, одна грань которого - произвольный n-угольник, а все остальные п граней - треугольники, имеющие общую вершину | |
S - вершина пирамиды; ABCD - основание пирамиды; ASAB, ASBC, ASCD, ASDA - боковые грани; SA, SB, SC, SD - боковые ребра; АВ, ВС, CD, AD - ребра основания; SO - высота, SO | |
Основание правильной пирамиды - правильный многоугольник, а основание высоты - центр многоугольника, SF - апофема, SF Площадь боковой поверхности правильной пирамиды Sбоков = mp, где m - апофема, р - полупериметр основания. Объем пирамиды V = | |
Решение задач
1. 1. В основании пирамиды SABC, изображенной на рис. 256, лежит прямоугольный треугольник ABC (
1. 2. В основе ABCD правильной пирамиды SABCD лежит квадрат со стороной 10 см. Высота SO пирамиды равна 12 см. Найдите площадь поверхности и объем пирамиды. (Ответ. 360 см2, 400 см3)
2. 3. Основание пирамиды - прямоугольник со сторонами 3 см и 5 см. Высота пирамиды 10 см. Найдите объем пирамиды. (Ответ. 50 см3)
3. 4. Найдите объем правильной четырехугольной пирамиды, каждое ребро которой равно а. (Ответ. а3)
4. 5. Боковые ребра треугольной пирамиды попарно перпендикулярны и имеют длины 3 см, 4 см и 5 см. Найдите ее объем. (Ответ. 10 см3)
5. 6. В правильной четырехугольном пирамиде боковое ребро равно 10 см. Найдите:
а) высоту пирамиды, если диагональ основания равна 16 см;
б) апофему пирамиды, если сторона основания равна 12 см.
1. 7. Найдите объем правильной четырехугольной пирамиды, боковое ребро которой равно 12 см и образует с высотой пирамиды угол 30°.
2. 8. Одна из самых величественных сооружений древности - пирамида Хеопса - имеет форму правильной четырехугольной пирамиды, высота которой равна 150 м, а боковое ребро - 220 м. Найдите площадь основания пирамиды. (Ответ. 51800 м2)
3. 9. На рис. 257 изображен развертку четырехугольной пирамиды, в основании которой лежит квадрат со стороной 6 см, боковые грани пирамиды - правильные треугольники. Найдите высоту пирамиды и ее объем. (Ответ. 3
1. 1. Изучить формулы площади поверхности и объема правильной пирамиды.
2. 2. Решить задачи.
3. 1) Найдите площадь поверхности правильной четырехугольной пирамиды, каждое ребро которой равно а.
4. 2) В основании пирамиды лежит ромб с диагоналями 6 см и 8 см. Высота пирамиды равна 10 см. Найдите объем пирамиды.
5. 3) Найдите объем правильной четырехугольной пирамиды, диагональ основания которой равна 4 см, а боковое ребро образует с высотой пирамиды угол 45°.
ОТВЕТИТЬ НА ВОПРОСЫ
1. 1. Что называется n-угольной пирамидой?
2. 2. Какая пирамида называется правильной?
3. 3. Какие свойства правильной пирамиды вам известны?
4. 4. Чему равна площадь поверхности пирамиды?
5. 5. Чему равна площадь боковой поверхности правильной пирамиды?
6. 6. Чему равен объем пирамиды?
УРОК №45
29.11.2022г. Группа 303. Математика. Тема. «Решение задач . Объёмы тел»
На прошлом уроке мы с вами ввели понятие объёма геометрических тел, записали формулы объёмов. Сегодня мы будем применять полученные знания для решения задач.
Решение задач
Самостоятельное решение:
УСПЕХА ВАМ!
УРОК №47-48
29.11.2022г. ГРУППА 303. Математика. Тема. «ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ И ОБЪЁМ ПРИЗМЫ»
Площадью боковой поверхности призмы называется сумма площадей всех боковых граней призмы.
Площадь боковой поверхности прямой призмы Sбок = Росн. Н
где H — высота призмы.
Площадь полной поверхности призмы — сумма площадей всех граней призмы.
Она состоит из площади боковой поверхности и площади оснований
Sполн.=Sбок.+2Sосн.
Все грани куба — квадраты, поэтому рациональнее использовать формулу
Sполн.пов. куба = 6⋅a2.
Объём прямой призмы находится по формуле:
V=Sосн..⋅H.
Для прямоугольного параллелепипеда можно использовать формулу V=abc , где a, b, c — измерения прямоугольного параллелепипеда (длина, ширина, высота).
Для куба используется формула V=a3, где a — ребро куба.
Основанием призмы может быть любой n-угольник, поэтому важно знать формулы вычисления их площадей.
Важные формулы нахождения площади n-угольников
Квадрат | a2 | | |
Прямоугольник | a⋅b | | |
Ромб | a⋅b⋅sinα | a⋅h | |
Параллелограмм | a⋅b⋅sinα | a⋅h | |
Равносторонний треугольник |
| | |
Прямоугольный треугольник | a⋅b/2 | a⋅h/2 | |
Произвольный треугольник | a⋅b⋅sinα2 | a⋅h2 | |
Трапеция | (a+b)/2⋅h | |
САМОСТОЯТЕЛЬНОЕ РЕШЕНИЕ ЗАДАЧ
Задача1.
Найдите объём прямоугольного параллелепипеда. Стороны основания которого равны a и b , а высота равна h , если:
А) a = 11 b = 12 h = 15
Б) a = 3
Задача 2.
Найдите объём куба АБСДА1Б1С1Д1 ,если а) АС = 12 см; б) ДЕ = 1 см, где Е – середина ребра АБ.
Задача 3.
Измерения прямоугольного параллелепипеда 8 см; 12 см; 18 см. Найдите ребро куба, объём которого равен объёму этого параллелепипеда.
Задача 4.
Найдите площадь боковой поверхности и объём прямой призмы АБСА1Б1С1, если
УРОК №
25.11.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА." РЕШЕНИЕ ЗАДАЧ, ТЕЛА ВРАЩЕНИЯ"
Практическая работа Решение задач
4. Какое количество нефти (в тоннах) вмещает цилиндрическая цистерна диаметра 18 м и высотой 7 м, если плотность нефти равна 0,85 г/см3?
H = 7м; d = 1м;
m =?
Vц =
m = V·ρ
Выполнить тест
1. Образующая конуса составляет с плоскостью основания угол 600, а радиус основания равен 9 см.
Найдите площадь полной поверхности конуса.
2. Площадь осевого сечения цилиндра равна 120 см2, а его образующая равна 10 см. Найдите объём цилиндра.
3. В каком случае потребуется больше краски: на покраску одного шара диаметром 10 см или на покраску 10 шаров диаметром 1 см
УРОК №46
28.11.2022г. ГРУППА 303. Математика. Тема. « Подобие
многогранников. Решение задач»
Два многогранника называются
подобными, если они имеют соответственно равные многогранные углы и
соответственно подобные грани.
Соответственные
элементы подобных многогранников называются сходственными. У подобных многогранников двугранные углы равны и
одинаково расположены; сходственные рёбра пропорциональны.
Если в пирамиде проведём секущую
площадь параллельно основанию, то она отсечёт от неё другую пирамиду, подобную
данной.
Поверхности подобных многогранников
относятся, как квадраты сходственных линейных элементов многогранников.
Объёмы подобных многогранников
относятся как кубы сходственных линейных элементов этих многогранников.
Квадраты объёмов подобных
многогранников относятся как кубы площадей сходственных граней.
Подобные цилиндры и
конусы.
Два цилиндра, конуса или усечённых
конуса называются подобными, если подобны их осевые сечения.
Боковые и полные поверхности
подобных цилиндров, конусов и усечённых конусов относятся, как квадраты их
сходственных линейных элементов. (радиусов оснований, высот, образующих).
Объёмы подобных тел.
Так как пирамиды Р1' и
Р1 подобны и коэффициент подобия равен k, то и отношение
их высот равно k, а отношение площадей их оснований равно k2.
Поэтому, отношение объёмов пирамид равно k3.
Число k – коэффициент подобия – равен
отношению расстояний между любыми двумя соответствующими парами точек при
преобразовании подобия. Поэтому, это число равно отношению любых двух
соответствующих линейных размеров тел Таким образом, мы приходим к
следующему выводу:
Объёмы двух подобных тел относятся
как кубы их соответствующих линейных размеров.
Квадраты объёмов подобных тел
относятся, как кубы площадей соответствующих граней.
Объёмы подобных цилиндров, конусов и
усечённых конусов относятся, как кубы их соответствующих линейных
элементов (радиусов оснований, высот, образующих).
Объёмы шаров относятся, как кубы их
радиусов или диаметров.
Практическая часть:
1. Высота
конуса равна 5 см. На расстоянии 2 см от вершины его
пересекает плоскость, параллельная основанию. Найдите объём исходного конуса,
если объём меньшего конуса, отсекаемого от исходного, равен 24 см3.
а)
325 см3;
б) 375 см3;
в)
385 см3;
г)
370 см3.
2.
Объём конуса равен 27. На высоте конуса лежит точка и делит её в
отношении 2 : 1 считая от вершины. Через точку проведено сечение,
которое является основанием меньшего конуса с той же вершиной. Найдите объём
меньшего конуса.
а) 8;
б)
4;
в)
6;
г)
5.
3. В
усечённой пирамиде соответственные стороны оснований относятся как 2 : 5.
В каком отношении делится её объём плоскостью, проходящей через середину высоты
этой пирамида параллельно основаниям ?
4. В
сосуде, имеющем форму конуса, уровень жидкости достигает 1/2
высоты. Объём жидкости равен 54 мл. Сколько миллилитров жидкости нужно
долить, чтобы полностью наполнить сосуд ?
а)
387 мл;
б)
383 мл;
в) 378
мл;
г)
373 мл.
5.
Объём конуса равен 16. Через середину высоты параллельно основанию конуса
проведено сечение, которое является основанием меньшего конуса с той же
вершиной. Найдите объём меньшего конуса.
а) 2;
б)
5;
в)
4;
г)
7.
6.
Объём конуса равен 10. Через середину высоты параллельно основанию конуса
проведено сечение, которое является основанием меньшего конуса с той же
вершиной. Найдите объём меньшего конуса.
а)
1,35;
б)
1,2;
в) 1,25;
г)
1,3.
7. В
сосуде, имеющем форму конуса, уровень жидкости достигает 1/2
высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить,
чтобы полностью наполнить сосуд ?
а)
480 мл;
б) 490
мл;
в)
495 мл;
г)
485 мл.
8. В
сосуде, имеющем форму конуса, уровень жидкости достигает 1/3
высоты. Объём жидкости равен 14 мл. Сколько миллилитров жидкости нужно
долить, чтобы наполнить сосуд доверху ?
а)
362 мл;
б)
360 мл;
в)
368 мл;
г)
364 мл.
9.
Дано: конус,
SО =
5 см, SО1 = 2 см.
Объём малого
конуса равен 24 см3 (см. рисунок). Найдите объём
большого конуса.
а) 375 см3;
б)
385 см3;
в)
370 см3;
г)
380 см3.
Задание:
1. Радиусы
оснований усечённого конуса относятся как 2 : 3. Высота конуса разделена
на три равные части, и через точки деления проведены плоскости, параллельные
основаниям. Найти в каком отношении разделился объём усечённого конуса.
а)
127 : 162 : 217;
б)
127 : 168 : 219;
в)
123 : 168 : 217;
г)
127 : 168 : 217.
2. Если
объёмы двух сфер относятся как 64 : 125, то площади их поверхностей
относятся как ?
а)
4 : 5;
б) 16 : 25;
в)
2 : 8;
г)
16 : 64.
УРОК №45
28.11.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «ПОНЯТИЕ ОБЪЁМА. КУБ. ПАРАЛЛЕЛЕПИПЕД. ПРИЗМА»
С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.
Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.
Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см3). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм3), кубический метр (1 м3) и тому подобное.
Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метров в бассейне и так далее.
Объём обозначается заглавной латинской буквой V.
Пример:
Объём книги 400 кубических сантиметров запишут: V = 400 см3.
Рассмотрим свойства объёмов.
Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.
Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Следствие из основных свойств объёмов.
Объём куба с ребром 1/n равен 1/n3
Объём прямоугольного параллелепипеда
Теорема
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
V = a ∙ b ∙ c..
Примеры и разбор решения заданий тренировочного модуля.
№1. Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.
Решение:
Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:
А теперь найдём объём параллелепипеда:
V = 15 ∙ 20 ∙ 25 = 7500 см3
Ответ: V = 7500 см3.
220 см2
100 см2
400 см2
200 см2
Решение.
Найдём длину АD:
AD = 960 : 8 : 20 = 6 см
Найдём АС, воспользовавшись теоремой Пифагора:
Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см2.
Ответ: площадь закрашенной фигуры 200 см2.
Задание 1. Вычислите объем куба с ребром 8 метров.
Решение. Просто возводим сторону ребро куба в третью степень:
Задание 2. Если ребро куба увеличить на 2 дм, то его объем вырастет на 98 дм3. Какова длина ребра этого куба?
Решение. Обозначим длину ребра буквой х. Тогда объем куба будет составлять х3 дм. Если ребро увеличить на 2 дм, то оно будет иметь длину х + 2 дм, и тогда объем куба будет равен уже (х + 2)3 дм.
Условие задачи можно записать в виде уравнения:
(х +2)3 = 98
Это квадратное уравнение имеет два корня, 3 и (– 5), что можно проверить с помощью теоремы Виета. Корень х = – 5 не имеет геометрического смысла, поэтому остается ответ х = 3. Ответ: 3 дм.
Далее рассмотрим перевод единиц измерения объема.
Например, как перевести 1 м3 в кубические сантиметры?
Рассмотрим куб с ребром 1 м. Ясно, что его объем будет равен 1 м3. С другой стороны, можно сказать, что длина ребра этого куба составляет 100 см: Тогда объем этого куба можно посчитать так: 1003 = 1000000 см3 Аналогично можно переводить и другие единицы измерения.
Привальная четырехугольная призма. Свойства правильной четырехугольной призмы. Основания правильной четырехугольной призмы – это 2 одинаковых квадрата;
Формулы для правильной четырехугольной призмы.
ЗАДАНИЕ 1. Составить таблицу, в которой указать площади боковой и полной поверхности, а также объёма куба, параллелепипеда, призмы. 2. Выполнить тест «Объёмы призмы» |

УРОК № 43-44
25.11.2022 г. ГРУППА 303. МАТЕМАТИКА. ТЕМА. «РЕШЕНИЕ ЗАДАЧ. ТЕЛА ВРАЩЕНИЯ»
Пользуясь представленной таблицей, вы сможете решить задачи на данную тему.
РЕШИТЕ САМОСТОЯТЕЛЬНО:
1. В цилиндре с радиусом основания 5см и высотой 10 см проведено сечение плоскостью, параллельной оси цилиндра на расстоянии 3 см от оси. Найдите площадь сечения.
2. Осевое сечение конуса – это треугольник с углом при вершине в 600 . Найдите отношение Sбок. : Sосн.
3. Сфера радиусом 5 см касается сторон треугольника с длинами 15 см, 15 см и 24 см. Найдите расстояние от центра сферы до плоскости треугольника.
ГРУППА №41-42
23 .11.2022 ГРУППА 303
МАТЕМАТИКА. ТЕМА « ШАР. СФЕРА»
Сферой называется поверхность, состоящая из точек пространства, расположенных на данном расстоянии от данной точки.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы, тоже называют радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Очевидно, диаметр сферы равен 2R.
Сфера может быть получена вращением полуокружности вокруг её диаметра.
Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
Уравнение сферы:
Расстояние от произвольной точки М (х; у; z) от точки С – центр сферы:
МС = (х – х0)2 + (у – у0)2 + (z0 - z0)2
Если точка М лежит на данной сфере, то МС = R, или МС2 = R2, т.е. координаты точки М удовлетворяют уравнению:
(х – х0)2 + (у - у0) + (z – z0)2 = R2
Если же точка М (х;у;z) не лежит на данной сфере, то МС2 =/ R2
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ СФЕРЫ И ПЛОСКОСТИ,
Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку. d = R
Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек. d ≥ R
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Для определения площади сферы пользуются понятием описанного
многогранника. За площадь сферы принимают предел последовательности площадей поверхностей этих многогранников.
Формула для вычисления площади сферы радиуса R:
S = 4π R2
Решение задач
.Пользуясь учебником Л.С.Атанасян «Геометрия 10-11» прочитать п. 64 «Сфера и шар» и зафиксировать в тетради ответы на вопросы. 1.Что называется сферой? 2.Скопировать рис. 157 и указать центр сферы и радиус. 3.Записать определение радиуса и сферы .4.Записать определение диаметра сферы 5.Вращением какой геометрической фигуры может быть получена сфера? 6.Что называется шаром? 7.Как бы вы ответили на вопрос: чем отличаются шар и сфера? 8.Запишите в тетрадь формулу площади сферы : Sсф.=𝟒𝝅𝑹2.
УРОК №-39-40
22.11.202г. ГРУППА 303 . МАТЕМАТИКА. ТЕМА " РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ТЕЛА ВРАЩЕНИЯ»
Решение задач по готовым чертежам
Задачи даются по нарастающей сложности:
1. Дано: Конус, ∠ABC = 120°, АВ = 6 (рис. 3).
Найти: R, Н.
Решение
1) ΔАВС - равнобедренный, угол при основании ∠A = ∠С = 30°.
2) Из ΔАВО Н = ВО = 3.
(Ответ: H = 3, R = 3√3.)
2. Дано: Конус. ΔАВС - равносторонний, АВ = 12, R = 10 (рис. 4).
Найти: OK, Н.
Решение:1) Из ΔВОС по теореме Пифагора
3. Высота конуса равна h. Через образующие МА и MB проведена плоскость, составляющая угол α с плоскостью основания. Хорда АВ стягивает дугу с градусной мерой β (рис. 5).
1) Докажите, что сечение конуса плоскостью МАВ - равнобедренный треугольник;
2) Объясните, как построить линейный угол двугранного угла, образованного секущей плоскостью и плоскостью основания;
3) Найдите МС;
4) Составьте (и объясните) план вычисления длины хорды АВ;
5) Составьте план вычисления площади сечения МАВ;
6) Покажите на рисунке, как можно провести перпендикуляр из точки плоскости сечения МАВ (обоснуйте построение)
Решение: 1) Образующие конуса равны. Следовательно, стороны ΔМАВ МА = MB, ΔМАВ - равнобедренный.
2) ΔАОВ - равнобедренный, так как две стороны - радиусы окружности. ΔАМВ - равнобедренный, так как две стороны-образующие конуса. Треугольники имеют общее основание. Значит, высоты этих треугольников имеют общую точку - середину основания АВ. По определению линейного угла: угол МСО - является линейным углом двугранного угла, образованного секущей плоскостью МАВ и плоскостью основания конуса.
4) Из ΔСОМ
6) Плоскость СОМ перпендикулярна плоскости ВАМ, т.к. одна из плоскостей (СОМ) проходит через перпендикуляр к другой (ВС). Поэтому перпендикуляр OO1 к прямой МС является перпендикуляром к плоскости ВАМ.
Решение задач
№ 1 (рис. 9)
Решение: 1. ABCD - квадрат.
2. Так как O1К - расстояние от точки О до ABCD, то О1К ⊥ ABCD, О1К ⊥ ВС.
3. АВ = ВС = 12 см ⇒ ВК = 6 см. 4. BO1 = 10 см.
5. ΔВКО1 - прямоугольный, по теореме Пифагора
- На этом уроке мы отрабатывали навыки решения задач на нахождение элементов цилиндра, конуса и совершенствовали полученные знания при решении задач. Самостоятельно решите из учебника "Геометрия 10-11"Автор Л.С.Атанасян - 617,,605
УРОК №37-38
21.11.2022г. ГРУППА 303. МАТЕМАТИКА.Тема "Тела вращения. Конус"
Историческая справка
Конус в переводе с греческого “konos” означает “сосновая шишка”. С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470-380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона (428-348 гг. до н.э.). Платон был учеником Сократа (470-399 гг. до н.э.). Он в 387 г. до н.э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: “Пусть сюда не входит никто, не знающий геометрии”. Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260-170 гг. до н.э.) – учеником Евклида (III в. До н.э.), который создал великий труд из 15 книг под названием “Начала”.
ОПРЕДЕЛЕНИЯ:
Тело, ограниченное конической поверхностью и кругом с границей L , называется конусом, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием – образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса.
Ось конической поверхности называется осью конуса, а её отрезок между вершиной и основанием – высотой конуса. Запомните, что все образующие конуса равны друг другу.
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.
Рассмотрим сечение конуса различными плоскостями. Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса – круг с центром О1, расположенным на оси конуса.
Боковую поверхность конуса можно развернуть на плоскость, разрезав её по одной из образующих. Развёртка боковой поверхности конуса – круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:
S = πrl
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания, поэтому формула площади полной поверхности конуса:
S = π r(l + r)
ЗАДАНИЕ:
1. Сделать конспект, выписав определения, зарисовав конус и указав основание, вершину, образующую, высоту конуса. (для этого можете обратиться к учебнику – «Геометрия 10-11), автор Л.С. Атанасян и др.) стр.135 параграф 61 – 62.
2. Решить задачи: №555, 561.
Решение задач на нахождение элементов конуса. (По готовым чертежам). (Слайд с 4 по 7)
ЗАПОЛНИТЕ ТАБЛИЦУ, РЕШИВ ЭТИ ЗАДАЧИ
| 1 | 2 | 3 | 4 | 5 |
l | | | 2 | 2 | |
r | 1,5 | | | 3 | |
h | 1,5 | | | | |
S | | | | 9 | |
a | | 300 | | |
l – образующая конуса, r – радиус его основания, h - высота, S – площадь осевого сечения, a – угол образующей с осью.
Оценка 5 – все выполнено верно.
Оценка 4 – допущено не больше двух ошибок.
Оценка 3 – допущено не больше четырех ошибок.
Оценка 2 – допущено больше четырех ошибок.
Дополнительная информация о конусе.
- В геологии существует понятие “конус выноса”. Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину.
- В биологии есть понятие “конус нарастания”. Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
- “Конусами” называется семейство морских моллюсков подкласса переднежаберных. Раковина коническая (2-16 см), ярко окрашенная. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи. Раковины используются как украшения, сувениры.
- По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1 000 000 жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, так как образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса. некоторые люди пытаются спрятаться от разрядов под деревом, но древо не проводник, на нем заряды накапливаются и дерево может быть источником напряжения.
- В физике встречается понятие “телесный угол”. Это конусообразный угол, вырезанный в шаре. Единица измерения телесного угла – 1 стерадиан. 1 стерадиан – это телесный угол, квадрат радиуса которого равен площади части сферы, которую он вырезает. Если в этот угол поместить источник света в 1 канделу (1 свечу), то получим световой поток в 1 люмен. Свет от киноаппарата, прожектора распространяется в виде конуса.
Итак, мы с вами познакомились с понятием конуса, его элементов и научились решать задачи на нахождение элементов конуса. Вопрос о конусе важен, так как конические детали имеются во многих машинах и механизмах. В автомобилях, танках, бронетранспортерах – конические шестерни; носовая часть самолетов и ракет имеет коническую поверхность.
Урок №35-36
18.11.2022г. ГРУППА 303. МАТЕМАТИКА. Тела вращения. Цилиндр. Сечения цилиндра.
Перечень вопросов, рассматриваемых в теме:
- тело вращения;
- цилиндрическая поверхность, её образующая; цилиндр, все его элементы и сечения;
- площади поверхностей цилиндра.
Цилиндрическая поверхность – это поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность.
Эти прямые – образующие цилиндрической поверхности.
Прямая, проходящая через центр окружности, перпендикулярно к плоскости – ось цилиндрической поверхности.
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами.
Круги – основания цилиндра; отрезки образующих, заключённые между основаниями – образующие цилиндра; образованная ими часть цилиндрической поверхности – боковая поверхность.
Ось цилиндрической поверхности называется осью цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Сечение – изображение фигуры, образованной рассечением тела плоскостью.
Осевое сечение – вариант сечения, при котором плоскость проходит через ось тела.
Развёртка боковой поверхности цилиндра – прямоугольник, одна сторона которого равна высоте цилиндра, а другая длине окружности основания.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций: базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
1. Основные определения
Определение
Цилиндрической поверхностью называется поверхность, образованная прямыми, проходящими через все точки окружности, перпендикулярными плоскости, в которой лежит эта окружность (см.рис.).
Определение
Сами прямые называют образующими цилиндрической поверхности.
Определение
Прямая,проходящая через точку О, перпендикулярно к плоскости, называется осью цилиндрической поверхности.
Так как все образующие и ось перпендикулярны плоскости 𝛂, значит они параллельны друг другу (вспомнить теорему «Если две прямые перпендикулярны к плоскости, то они параллельны»).
Если построить ещё одну плоскость 𝛃, которая будет параллельна плоскости 𝛂, то отрезки образующих, заключённые между плоскостями 𝛂 и 𝛃 будут параллельны и равны друг другу (вспомнить свойство параллельных плоскостей «отрезки параллельных прямых, заключённые между параллельными плоскостями, равны»). Точки, являющиеся концами отрезков параллельных прямых и лежащие в плоскости 𝛃, дают окружность, равную окружности, лежащей в плоскости 𝛂.
Определение
Тело, ограниченное цилиндрической поверхностью и двумя кругами (границы которых есть те самые равные окружности в плоскостях 𝛂 и 𝛃) называется цилиндром.
Определение
Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, - образующими цилиндра, а образованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра.
Определение
Ось цилиндрической поверхности называется осью цилиндра.
Определение
Длина образующей называется высотой цилиндра (все образующие равны и параллельны), а радиус основания – радиусом цилиндра.
Также цилиндр можно получить вращением прямоугольника вокруг одной из сторон. Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью цилиндра, противоположная сторона будет образовывать боковую поверхность, а две оставшиеся стороны образуют верхнее и нижнее основания, одновременно являясь радиусами цилиндра.
2. Сечения цилиндра различными плоскостями
Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.
Основные формулы
Формула для вычисления площади боковой поверхности цилиндра: Sбок=2𝛑RL.
То есть площадь боковой поверхности равна произведению длины окружности основания цилиндра на его высоту.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. В виде формулы это можно записать так: Sполн=2𝛑R(R+L).
Примеры и разбор решения заданий тренировочного модуля
1. Дан цилиндр.
Выберите значение площади его боковой поверхности
1) 60π
2) 192π
3) 120π
4) 36π
Решение:
Площадь боковой поверхности вычисляется по формуле: S=2πRL.
R=6, L=10
Подставим: S=2π·6·10=120π.
Ответ: 3) 120π
2. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу 1200. Образующая цилиндра равна 6
Решение:
Сделаем чертеж:
По условию задачи ∟АОВ=1200, ВС= 6
Расстояние от оси до секущей плоскости - отрезок ОН=1.
Найдем сторону АВ сечения.
∆ОНВ - прямоугольный.
В ∆ОНВ: ОН=1, ∟НОВ=600.
НВ=ОН·tg600=1·
Sсеч=6
Ответ: 18
3. Высота цилиндра на 6 больше его радиуса, площадь полной поверхности равна 144π. Найдите его образующую.
Решение:
Sполн =2πR(R+L)
По условию задачи L=R+6.
144π=2πR(R+R+6).
Получили квадратное уравнение относительно радиуса:
R2+6R-72=0
R=-12 или R=6. Так как длина радиуса не может быть отрицательной, получаем значение: R=6. Тогда образующая цилиндра равна 12.
Ответ: 12.
ЗАДАНИЕ:
1.Запишите в тетрадь все определения, зарисуйте необходимые рисунки.
2. Решить самостоятельно задачи: № 523, 529 на стр. учебника 133.
УРОК № 34
18.11.2022г. ГРУППА 303 МАТЕМАТИКА Контрольная работа №2 по теме «Многогранники»
Вариант 2.
Часть 1.
А1. Какие из данных фигур являются пирамидами?
А2.
Плоскость, проходящая через три точки A, B и С, разбивает правильную треугольную призму на два многогранника. Сколько рёбер у многогранника, у которого больше вершин?
1)13 2)12 3)10 4)9
А3. Найдите площадь поверхности многогранника, изображенного на рисунке (все углы прямые)
В1. В правильной четырёхугольной призме сторона основания равна 10, а боковое ребро АА1=2. Точка О принадлежит ребру А1В1 и делит его в отношении 4:1, считая от вершины А1 . Найдите площадь сечения этой призмы плоскостью, проходящей через точки А,С и О.
В2. Стороны основания правильной четырёхугольной пирамиды равны 42 см, боковые рёбра равны 75. Найдите площадь поверхности этой пирамиды.
УРОК №32-33
.11.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «РЕШЕНИЕ ЗАДАЧ»
Для решения задач по теме необходимо вспомнить:
- какой многогранник называется усечённой пирамидой?
- вспомнить элементы усечённой пирамиды: основания (верхнее, нижнее), высота, апофема, центры пирамиды и как их можно определить.
- знать формулы боковой и полной поверхности пирамиды
-знать формулы теоремы Пифагора, свойства правильного треугольника.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?
Решение
Поскольку в пирамиде все боковые грани равны, то и площади их будут равны. Знаем, что площадь боковой грани на 15 меньше площади основания, значит она равна 27. В пятиугольной пирамиде боковых граней 5.
Таким образом, площадь полной поверхности равна 27∙5+42 = 177.
Ответ: 177
Задание 2. В правильной пирамиде высота боковой грани равна 10, а в основании лежит квадрат со стороной 4. Чему равна площадь боковой поверхности?
Решение
Боковая грань пирамиды – это треугольник. Все боковые грани этой пирамиды равны между собой, так как пирамида правильная. Вычислим площадь треугольника: ½∙4∙10=20.
В основании пирамиды лежит квадрат, значит боковых граней будет 4. Таким образом, площадь боковой поверхности равна 4∙ 20=80.
Ответ: 80
№ 268
Дано: MABCD - правильная пирамида, А1В1С1 || АВС, МО1 : O1O = 1 : 2, NK - апофема, NK = 4 дм, Syc.пиp. = 186 дм.
Найти: ОО1 - ?
Решение: Рассмотрите ΔМКО. Так как NO1 || KO, то МО11 : МО = O1 N : OK, значит, стороны В1 С1 : ВС = МО1 : МО. В1 С1 = 1 : 3. Пусть В1 С1 = х, ВС = 3х. Имеем
(не удовлетворяет условию задачи); В1 С1 = 3 (см), NО = 1,5 (см); ВС = 9 (см), ОК = 4,5 (см); KF = OK – NO1 = 3. Из ΔKNF по теореме Пифагора
(Ответ: √7 дм.)
№ 269.
Дано: АВСА1 В1 С1 — усеченная пирамида. АВ = ВС = АС = 4 см; A1 B1 = B1 C1 = A1 C1 = 2 см; АА1 = 2 см. Найти: МК- ? A\F\ - ?
Решение: Пусть О и О1 - центры оснований пирамиды.
1) Из ΔАВС имеем: АВ = R√3, R = АО.
2) Из ΔА1 B1 C1 находим
3) EK = ОK - OE, ОЕ = O1 М, отсюда
5) Из ΔМЕК имеем: МК2 =МЕ2 +ЕК2 МК =
= (Ответ: ![]() )
)
ЗАДАНИЕ: выполнить самостоятельно
Вариант I
1. Из данных утверждений выберите верное: а) все ребра правильной пирамиды равны; б) площадь поверхности пирамиды равна половине произведения периметра основания на апофему; в) боковые грани усеченной пирамиды - трапеции; г) утверждения a-в не верны.
2. Найдите площадь боковой поверхности пирамиды, все грани которой наклонены к основанию под углом 60°, а в основании лежит прямоугольный треугольник с катетами 3 см и 6 см.
а) 9 см2, б) 10 см2, в) 12 см2, г) другой ответ.
3. В правильной четырехугольной пирамиде сторона основания равна 5 см, а плоский угол при вершине пирамиды 60°. Найдите боковое ребро пирамиды
4. В основании пирамиды SABC лежит равнобедренный треугольник ABC, в котором ВС = 12 см, а АВ = АС = 10 см. Найдите площадь сечения ASM, если оно перпендикулярно плоскости основания, а все боковые ребра пирамиды равны 10 см.
а)
б)
в) 31 см2, г) другой ответ.
5. Боковые ребра пирамиды SABC равны между собой. SD - высота пирамиды. Точка D лежит внутри ΔABC. ТреугольникABC:
а) прямоугольный;
б) остроугольный;
в) тупоугольный;
г) недостаточно данных.
6. Найдите площадь диагонального сечения правильной усеченной четырехугольной пирамиды, если ее высота равна √2 см, а стороны основания 1 см и 4 см.
а) 10 см2, б) 2,5 см2, в) 5 см2, г) другой ответ.
14.11.2022г. ГРУППА 303. МАТЕМАТИКА, ТЕМА. «ПОНЯТИЕ О ПРАВИЛЬНЫХ МНОГОГРАННИКАХ»
Выпуклый многогранник называется правильным, если все его грани - равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.
Отметим, что поскольку все грани - равные правильные многоугольники, то все ребра правильного многогранника равны.
Вам уже известны примеры некоторых правильных многогранников. Например, куб. Все его грани - равные квадраты и к каждой вершине сходится три ребра.
Также нам уже знаком правильный тетраэдр.
Заметьте, что правильный тетраэдр и правильная треугольная пирамида – это различные многогранники!
Напомним, что пирамида называется правильной, если в основании лежит правильный многоугольник, а основание высоты совпадает с центром многоугольника. Таким образом, в правильной треугольной пирамиде боковые ребра равны друг другу, но могут быть не равны ребрам основания пирамиды, а в правильном тетраэдре все ребра равны.
Правильных многогранников существует всего 5. Перечислим их.
Правильный тетраэдр – многогранник, составленный из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников, значит сумма плоских углов при каждой вершине равна 180.
Рисунок 1 - Правильный тетраэдр
Правильный октаэдр – многогранник, составленный из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников, значит, сумма плоских углов при каждой вершине равна 240.
Рисунок 2 - Правильный октаэдр
Куб (гексаэдр) – многогранник, составленный из шести квадратов. Каждая вершина куба является вершиной трех квадратов, значит, сумма плоских углов при
каждой вершине равна 270.
Рисунок 3 - Куб
Правильный икосаэдр – многогранник, составленный из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников, значит, сумма плоских углов при каждой равна 300.
Рисунок 4 – Правильный икосаэдр
Правильный додекаэдр – многогранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников, значит, сумма плоских углов при каждой равна 324.
Название каждого правильного многогранника происходит от греческого наименования «эдра» - грань; «тетра» - 4; «гекса» - 6; «окта» - 8; «икоса» - 20; «додека» -12.
Докажем, что правильных многогранников существует ровно 5, то есть что не существует правильного многогранника, гранями которого являются правильные n-угольники при n≥6.
Действительно, угол правильного n-угольника при n≥6 не меньше 1200. С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани - правильные n-угольники при n≥6, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше 3600. Но это не возможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 3600.
По этой причине каждая вершина правильного многогранника может быть вершиной либо трех, либо четырех, либо пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников.
Симметрия в пространстве
Одно из интересных свойств правильных многогранников – это элементы симметрии.
Прежде чем мы их выделим давайте определим симметрию в пространстве.
Вам уже знакома симметрия из курса планиметрии. Там мы рассматривали фигуры симметричные относительно прямой и точки. В стереометрии же рассматривают симметрию относительно точки, прямой и плоскости.
Будем говорить, что точки А и А1 симметричны относительно точки О (рис. 6), если О – середина отрезка АА1. В таком случае О будет являться центром симметрии и будет симметрична сама себе.
Рисунок 6 – Центральная симметрия
Точки А и А1 называются симметричными относительно прямой а, если прямая а проходит через середину отрезка АА1 и перпендикулярна к этом отрезку (рис. 7). Прямая а называется осью симметрии, а каждая ее точка считается симметричной самой себе.
Рисунок 7 – Осевая симметрия
Точки АА1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку (рис. 8). Плоскость α называется плоскостью симметрии, а каждая ее точка считается симметричной самой себе.
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.
Рисунок 8 – Зеркальная симметрия
Рисунок 9 – Элементы симметрии куба
Примером фигуры, обладающей и центральной, и осевой и зеркальной симметрией является куб (рис. 9).
Фигура может иметь один или несколько центров (осей, плоскостей) симметрии. Так, например, у куба один центр симметрии и несколько осей и плоскостей симметрии.
В геометрии центр, ось и плоскость симметрии многогранника называют элементами симметрии многогранников.
С симметрией мы часто можем встретиться в природе, архитектуре, быту.
Например, многие кристаллы имеют центр ось или плоскость симметрии.
Многие здания симметричны относительно плоскости. Примером такого здания является здание Московского государственного университета.
Примеры и разбор решения заданий тренировочного модуля
№1 Выберите неверные утверждения
1) правильный додекаэдр состоит из 8 правильных треугольников
2) тетраэдр имеет 4 грани
3) гексаэдр состоит из шести параллелограммов
4) правильный октаэдр состоит из правильных пятиугольников
Решение
Утверждение под номером 1 неверно, так как название «додекаэдр» с греческого означает «двенадцать граней». В действительности, додекаэдр состоит из двенадцати правильных пятиугольников.
Утверждение 2 верно. Тетраэдр с греческого означает 4 грани и состоит тетраэдр из 4-х треугольников.
Гексаэдр, он же куб состоит из квадратов, которые в свою очередь являются параллелограммами, поэтому утверждение 3 верно.
С греческого «октаэдр» означает 8 граней, состоять в таком случае из пятиугольников он не может. Октаэдр состоит из восьми треугольников. Утверждение 4 неверно.
Ответ: 1 и 4
№ 2 Установите соответствие между правильными многогранниками и их развертками.
1)
Для выполнения этого задания необходимо понять, из каких многоугольников составлен многогранник.
Итак, куб состоит из квадратов. Единственная развертка, состоящая из квадратов это развертка под номером 6. Проверить себя можно и мысленно сложив из развертки кубик.
Многогранник под номером 2 – тетраэдр, состоит из четырех треугольников. Поэтому ему будет соответствовать развертка под номером 7. Мысленно сложите из развертки тетраэдр.
Октаэдр состоит из 8 треугольников, в этом несложно убедиться исходя из изображения. Развертка под номером 8 как раз состоит из 8 треугольников.
Многогранник под номером 4 состоит также из треугольников, а единственная развертка, состоящая из треугольников, осталась под номером 10. Попробуйте вырезать такую развертку из бумаги и собрать свой икосаэдр!
Многогранник под номером 5 состоит из пятиугольников. Оставшаяся развертка 9 тоже состоит из пятиугольников. Осталось проверить, что количество совпадает.
Ответ: 1 и 6, 2 и 7, 3 и 8, 4 и 10, 5 и 9
Задание. Вычислите площадь поверхности икосаэдра, если его
ребро имеет длину 1.
Решение. Найдем площадь одной грани
икосаэдра. Она представляет собой равносторонний треугольник со стороной 1. Удобно вычислить
его площадь по формуле Герона.
Сначала
найдем полупериметр треугольника: 1
Решение. Найдем площадь одной грани икосаэдра. Она представляет собой равносторонний треугольник со стороной 1. Удобно вычислить его площадь по формуле Герона.
Сначала
найдем полупериметр треугольника:
Р = 1+1+1/2
= 1,5
Далее используем саму формулу Герона:
Sграни =
Так как у
икосаэдра 20 граней, то надо лишь умножить полученный результат на 20, чтобы
вычислить полную площадь икосаэдра:
S = 20∙Sграни = 20∙0,25
Ответ: S = 5
УРОК № 28-29
11.11.2021г ГРУППА 303 . ТЕМА. «Сечения многогранников».
Перечень вопросов, рассматриваемых в теме:
- Решение задач, сводящихся к доказательству, связанному с построением сечения многогранника
- Построение сечения многогранников
- Решение задач на нахождение площадей сечений многогранников
Площадь
треугольника S=½hа
трапеции S=½h(а+b)
параллелограмма S=hа
Основная литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.
Открытые электронные ресурс:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются. Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.
Теорема о параллельности трех прямых: если a∥b, b∥c, то и a∥c. Определение: прямая и плоскость параллельны, если они не имеют общих точек.
Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.
Определение: две плоскости параллельны, если они не имеют общих точек.
Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.
Если две плоскости пересекаются, то их линия пересечения — прямая.
Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)
Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника.
№1 SABCD – четырехугольная пирамида, в основании которой лежит квадрат ABCD, а две боковые грани SAB и SAD представляют собой прямоугольные треугольники с прямым углом ∠A. Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.
Решение: сначала построим сечение по условию задачи.
1)Пусть AC∩BD=O. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Заметим, что т.к. ∠SAB=∠SAD=90∘⇒SA⊥(ABC). Проведем в плоскости SAC прямую OK∥SC. Т.к. O – середина AC, то по теореме Фалеса K – середина SA. Через точку K в плоскости SAB проведем KM∥SB (следовательно, M – середина AB). Таким образом, плоскость, проходящая через прямые OK и KM, и будет искомой плоскостью.
Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M, получим прямую MN. Т.к. α∥(SBC),то α пересечет плоскость SCD по прямой NP∥SC (если NP∩SC≠∅, то α∩(SBC)≠∅, что невозможно ввиду их параллельности). Таким образом, KMNP – искомое сечение, причем KP∥AD∥MN⇒ это трапеция.
![]() 2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN. Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3
2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN. Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3![]() a2/8
a2/8
Ответ:3![]() a2/8
a2/8
№2 Найди площадь сечения прямой призмы, проходящей через середины ребер, если
=120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см2 .
боковая грань прямой призмы является прямоугольником.
Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.![]()
То есть большая боковая грань содержит большую сторону основания.
По условию
=120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов
Получим, что длина стороны АС=7см.
Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.
Получим, что длина высоты призмы равна
.Найдем площадь основания, а оно равно площади
сечения, по формуле .
Мы воспользуемся второй формулой. Получим, что площадь основания равна
.№3 На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:QB=1:2. Точка P — середина ребра AS.
Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
Решение:
пусть сторона основания пирамиды равна 3а, а высота пирамиды равна h. Тогда площадь сечения DSB равна
![]() S=BD*SO/2= 3 =6
S=BD*SO/2= 3 =6
откуда ah=2 .
Площадь сечения DPQ равна
№4
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M, АВ=4, АА1=6. Найдите площадь сечения.
Решение:
По теореме о трех перпендикулярах прямые BM и AC перпендикулярны, а значит, прямые BM и KL перпендикулярны. Площадь четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей. Найдем их: KL=AC=4 как диагональ квадрата, лежащего в основании призмы по теореме Пифагора.
Тогда
ЗАДАНИЕ:
1. Задача 1. Построить сечение куба плоскостью, проходящей через точки: A1; M ∈ B1C1; N ∈ AD.
УРОК № 26-27
07.11.2022г. ГРУППА 303 МАТЕМАТИКА. ТЕМА «СЕЧЕНИЯ КУБА»
Плоскость может пересекать минимум три ребра, и тогда в сечении получается треугольник (см. рис. 37). Меняя наклон плоскости можно получить равнобедренный или даже равносторонний треугольник.
Рис. 37. Сечение куба – треугольник
Если плоскость параллельна грани, то в сечении получим квадрат (см. рис. 38).
Рис. 38. Сечение куба – квадрат
Если секущая плоскость параллельна ребру, то получим прямоугольник (см. рис. 39).
Рис. 38. Сечение куба – прямоугольник
Если совсем избавиться от параллельности ребру или грани, то получим параллелограмм (см. рис. 39).
Рис. 39. Сечение куба – параллелограмм
Озвученные выше утверждения мы сможем доказать чуть позже, когда докажем, что плоскость пересекает две параллельные плоскости по параллельным прямым.
Секущая плоскость может пересекать 5 или все 6 граней. В сечении будут получаться пятиугольник (см. рис. 40) или шестиугольник (см. рис. 41).
Рис. 40. Сечение куба – пятиугольник
Рис. 41. Сечение куба – шестиугольник
Построение сечения куба
Решим задачу: Построить сечение куба
Сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат ребрам, а стороны - граням многогранника.
При построения сечения для нас важно, что две соседние вершины сечения должны принадлежать одной грани многогранника. Отрезок, соединяющий вершины, не лежащие в одной грани, не является стороной сечения.
В этой задаче ни одна пара точек, через которые мы должны провести сечение, не лежит в одной грани куба, поэтому мы не можем соединить никакие две из данных точек отрезком, чтобы найти сторону сечения.
В этом случае для построения сечения мы введем вспомогательную плоскость.
Мы введем вспомогательную плоскость следующим образом.
Найдем ортогональную проекцию точки К на плоскость основания куба, получим точку
и LCпроведем вспомогательную плоскость K 1KL (голубая плоскость). Точка N - точка пересечения прямых KL и K1 C и, следовательно, она лежит в плоскости искомого сечения и в плоскости основания.
Прямая MN лежит и в плоскости сечения, и в плоскости основания куба, поэтому точка R -точка пересечения прямой ![]() с ребром
с ребром ![]() является вершиной сечения, лежащей в одной грани с вершиной М.
является вершиной сечения, лежащей в одной грани с вершиной М.
Мы нашли стороны сечения МК и КL:
Самую сложную часть решения мы прошли. Дальше проще. Соединим полученные точки прямыми - мы получим искомое сечение KLRM
ЗАДАНИЕ:
Задача 1. Построить сечение куба АВСДА1В1С1Д1, проходящего через точки МNД1
УРОК № 24-25
.11.2022г. ГРУППА 301. МАТЕМАТИКА. ТЕМА «СЕЧЕНИЕ ПИРАМИДЫ»
Сечение пирамиды плоскостью представляет собой плоскую фигуру и содержит в себе точки принадлежащие как поверхности пирамиды так и секущей плоскости. Пирамида это многогранник - геометрическое тело боковой поверхностью которого служат плоские грани в виде треугольников.
ВИДЫ СЕЧЕНИЙ:
1. Диагональное сечение- – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):
На данном рисунке:
- пирамиды ЕАВСД и Е1А1В1С1Д1 подобны
- четырёхугольники АВСД и А1В1С1Д1 подобны.
Примечание: существуют и другие виды сечений.
Пошаговое построение сечения: треугольная пирамида.
В этой статье мы построим несколько сечений треугольной пирамиды, будем при этом использовать метод следов. Сначала мы рассмотрим самые простые случаи: когда точки, через которые должно пройти сечение, принадлежат ребрам пирамиды. Потом – случаи сложнее, когда одна или две из точек плоскости сечения принадлежат граням пирамиды. Поехали!
Задача 1. Построить сечение пирамиды, проходящее через точки P, Q, R.
Сначала надо попробовать отыскать такие точки, которые принадлежат одной плоскости. У нас это точки P и Q – они принадлежат грани ASC, а
Также пара Р и R – они принадлежат грани АВС. Их можно сразу соединять.
Шаг 1
Теперь, чтобы понять, как плоскость рассечет грань SBC, нужно заполучить точку в этой грани, или в плоскости, которой принадлежит грань. Но нужна нам не любая, а особенная точка, которая также будет принадлежать и плоскости сечения. Чтобы точка принадлежала плоскости нужно, чтобы она принадлежала прямой этой плоскости. Заметим, что прямая PR лежит в плоскости основания и принадлежит искомому сечению. Прямая CB тоже лежит в плоскости основания, но не только. Она еще лежит в плоскости грани SBC, где нам необходима точка, чтобы построить сечение. Воспользуемся случаем: найдем точку, где прямые PR и CB пересекутся. Такая точка принадлежит сечению, а также плоскостям боковой (SBC) и нижней (ABC) граней пирамиды.
Шаг 2
Так как построенная точка T и точка Q лежат в одной плоскости, то можем соединить их прямой
Шаг 3
Эта прямая пересечет ребро SB в точке F – это и есть еще одна нужная нам точка для построения сечения. Соединяем R и F – они лежат в одной плоскости (SAB). Теперь смотрим: можно ли пройти по линиям сечения, принадлежащим граням пирамиды, от точки P и снова попасть в нее непрерывным маршрутом? Если да, то построение окончено. У нас такой маршрут замкнутый: P-Q-F-R-P. Это и есть сечение.
Шаг 4
Задача 2. Построить сечение пирамиды, проходящее через точки P, Q, R
Дано
Видим, что точки R и Q принадлежат одной грани пирамиды – SCB – и соединяем их.
Шаг 1
Можно, конечно, было бы сразу и точки P и Q соединить – они тоже лежат в одной плоскости – плоскости грани SAB. Но это успеется, пока что нам нужна точка в плоскости грани SAC, да такая, чтобы принадлежала и сечению. Поэтому она должна принадлежать прямой искомого сечения, и прямой, принадлежащей плоскости SAB, то есть быть пересечением таких прямых. Продлим SC до пересечения с прямой QR -и получим такую точку.
Шаг 2
Точка X и точка P принадлежат одной плоскости, можем их соединить и получить точку пересечения данной прямой с ребром AC:
Шаг 3
Соединяем E с R, P с Q, и получаем сечение
Шаг 4.
Задача 3. . Построить сечение пирамиды, пролходящей через точки SPRQ
Дано
Теперь, уже имея опыт, первый шаг выполняем без проблем:
Шаг 1.
Понимаем, что нет точки в задней грани. Вернее, одна есть – P – но второй не хватает. Аналогично, есть одна точка в нижней грани – в плоскости основания, а второй точки нет. Определим такую точку: пересечем AC и PQ. Обе прямые лежат в плоскости SAC, PQ принадлежит плоскости сечения, поэтому их пересечение будет принадлежать обеим плоскостям:
Теперь имеем две точки в плоскости основания – U и R, и можем смело соединять их:
Шаг 3
Прямая UR пересечет ребро AB в точке Z. Теперь маршрут Q-R-Z-P-Q замкнут, можем достраивать сечение:
ЗАДАНИЕ:
Постройте сечение четырёхугольной пирамиды:
31 .10.2022г. ГРУППА 301. МАТЕМАТИКА . ТЕМА «СЕЧЕНИЕ ПРИЗМЫ ПЛОСКОСТЬЮ»
Ребята!
Тема представлена в виде презентации. Внимательно читайте их. Ответы на
вопросы вы найдёте в текстах презентации.
ЗАДАНИЕ:
Сделайте конспект урока, ответив на вопросы
1. Что называется плоским сечением?
2. Что называется сечением призмы?
3. От чего зависит вид сечения?
4. Чем являются сечения призмы, параллельные боковым рёбрам?
5. Что называется диагональным сечением призмы?
6. Что значит построить сечения?
7. Назовите методы построения сечения?
Примечание. Ответы сопровождайте рисунками.
УРОК № 21
28 .10.2022г. ГРУППА 303. Контрольная работа № 1 по теме «Многогранники»
К-5, Вариант 1
1. Сторона основания правильной четырёхугольной пирамиды равна а. Двугранные углы при основании равны α. Найдите площадь полной поверхности пирамиды.
2. В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 см и 6 см. Найдите боковое ребро призмы, если площадь её боковой поверхности составляет 120 см2.
3. Стороны основания прямого параллелепипеда равны 3 см и 5 см, угол между ними равен 60°. Большая диагональ параллелепипеда равна 10 см. Найдите боковое ребро параллелепипеда.
К-5, Вариант 2
1. Боковое ребро правильной четырёхугольной пирамиды равно 12 см и образует с плоскостью основания угол в 60°. Найдите площадь боковой поверхности пирамиды.
2. Найдите площадь поверхности прямоугольного параллелепипеда, стороны основания которого равны а и b, а диагональ образует с плоскостью основания угол α.
3. В основании прямой призмы лежит равнобедренный треугольник с основанием, равным 5 см. Высота призмы равна 3 см. Найдите площадь сечения призмы плоскостью, проходящей через основание равнобедренного треугольника и противоположную вершину верхнего основания призмы, если диагонали равных боковых граней равны 6,5 см.
К–5, Вариант 3
1. Сторона основания правильной четырёхугольной пирамиды равна а, высота равна b. Найдите площадь полной поверхности пирамиды.
2. В прямой треугольной призме стороны основания относятся как 17 : 10 : 9, а боковое ребро равно 16 см. Найдите стороны основания, если боковая поверхность призмы равна 1152 см2.
3. Основанием прямого параллелепипеда служит ромб с диагоналями 6 см и 8 см. Диагональ боковой грани равна √61 см. Найдите большую диагональ параллелепипеда.
К-5, Вариант 4
1. Высота боковой грани правильной четырёхугольной пирамиды равна 10 см. Определите площадь её полной поверхности, если боковая грань образует с плоскостью основания угол 60°.
2. Основанием прямого параллелепипеда является ромб со стороной а и острым углом α. Найдите площадь полной поверхности параллелепипеда, если его меньшая диагональ составляет с плоскостью основания угол β.
3. Стороны основания треугольной пирамиды равны 6 см, 10 см и 14 см. Плоскости боковых граней образуют с плоскостью основания угол 60°. Найдите полную поверхность пирамиды.
УРОК № 19-20
21.10.2022г. ГРУППА 303. МАТЕМАТИКА. ПРАКТИЧЕСКАЯ РАБОТА Решение задач по теме: «Многогранники».
1) теоретический материал:
Многогранник — это такое тело, поверхность которого составлена из многоугольников. Эти многоугольники называются гранями многогранника, их стороны — ребрами, а вершины — вершинами многогранника.
Пирамида — это многогранник, у которого одна грань, называющаяся основанием пирамиды, — многоугольник (любой), а другие грани — треугольники, выходящие из одной точки, которая называется вершиной пирамиды.
Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Отрезок, проведенный из вершины к основанию пирамиды и перпендикулярный плоскости основания, называется высотой пирамиды.
Пирамида называется правильной, если ее основание — правильный многоугольник, а высота проходит через центр основания.
Высота боковой грани правильной пирамиды, проведенная из его вершины, называется апофемой.
Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.
Обычно вершины обозначают так, что ABC... — это вершины основания, A1B1C1... — вершины второго основания, а AA1, BB1, ... — это боковые ребра.
Все боковые грани призмы — параллелограммы. Основания призмы равны друг другу.
Высотой призмы называется отрезок, являющийся общим перпендикуляром к плоскостям, в которых лежат основания призмы.
Если боковое ребро образует с плоскостью угол α, то высоту можно найти по формуле: h=asinα, где a — длина бокового ребра. Это следует из соотношения между гипотенузой и катетом в прямоугольном треугольнике (а — гипотенуза, h — это катет, а α — противолежащий угол).
Поверхность призмы складывается из боковых граней и двух оснований.
Легче всего искать площадь боковой поверхности и объем, когда боковые ребра перпендикулярны основанию, поскольку у такой призмы боковые ребра равны высоте призмы, а все боковые грани являются прямоугольниками.
Призма, у которой боковые ребра перпендикулярны основанию, называется прямой призмой.
Площадь боковой поверхности равна Sбок=Ph, где P — периметр основания
Правильной призмой называется прямая призма, у которой основание — правильный многоугольник.
У правильной призмы все боковые грани — равные прямоугольники. Площадь ее боковой поверхности равна Sбок=nha, где a — ребро основания, h — это высота призмы (она же боковое ребро призмы), а n — количество вершин основания.
Параллелепипед — это призма, основанием которой служит параллелограмм.
Прямоугольный параллелепипед — это параллелепипед, все грани которого — прямоугольники.
Куб — это прямоугольный параллелепипед, у которого все ребра равны.
2) задания для практической работы:
1. В прямоугольном параллелепипеде стороны основания равны 12см и 5см.
Диагональ параллелепипеда образует с плоскостью основания угол 45![]() .
.
Найдите площадь боковой поверхности параллелепипеда
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота 12см. Найдите площадь полной поверхности пирамиды
3. Найдите сторону основания и высоту правильной четырёхугольной призмы, если Sполн=90см2,
Sбок=40см2.
4. В правильной четырёхугольной пирамиде высота равна 12см, а апофема - 15см. Найдите площадь полной поверхности пирамиды.
5. Сторона основания правильной четырёхугольной пирамиды равна 12см, а высота пирамиды 12 см. Найдите боковое ребро пирамиды.
6. В основании прямой призмы ABCDA1B1C1D1 лежит параллелограмм со сторонами 3см и 6см и углом между ними 60![]() . Диагональ B1D образует с плоскостью основания угол 30
. Диагональ B1D образует с плоскостью основания угол 30![]() . Найдите площадь боковой поверхности призмы.
. Найдите площадь боковой поверхности призмы.
Кроссворд.
1. Высота боковой грани правильной пирамиды.
2.Точка, не лежащая в плоскости основания пирамиды.
3. Перпендикуляр, опущенный из вершины пирамиды к основанию.
4. Многоугольники, из которых составлен многогранник.
5. Не боковая грань.
6.Другое название куба.
7.Многогранник, состоящий из многоугольника, называемого основанием, точки, не лежащей в плоскости этого многоугольника, называемой вершиной, и всех отрезков, соединяющих вершину с точками основания.
8. Геометрическое тело, состоящее из четырёх одинаковых равносторонних треугольников.
9. Высота многогранника - это :
10. Параллелепипед, у которого боковое ребро не перпендикулярно к основанию называется :
11.Как называется многогранник, у которого два равных основания и n боковых граней - параллелограммов?
12. Назовите правильный многогранник, у которого больше всех граней.
13. Как называется призма, у которой боковые рёбра перпендикулярны основанию, а в основании лежит правильный многоугольник?
3) отметки :критерии
«3» ставится при решении кроссворда;
«4» - за задачи №1-3;
«5» - за задачи №1, №4-6.
УРОК № 18
21..10.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА. "Усеченная пирамида"
На прошлых уроках мы работали с пирамидами. Давайте вспомним, какой многогранник называется пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.
Многогранник, составленный из n –угольника и n- треугольников, называется пирамидой.
Пирамида называется правильной, если ее основание – правильный многоугольник.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Пусть нам дана пирамида PA1A2…An. Проведем секущую плоскость β, параллельную плоскости основания пирамиды и пусть эта плоскоспересекает боковые ребра в точках B1,B2,…, Bn.
Плоскость β разбивает пирамиду на две фигуры: пирамиду PB1B2…Bn и многогранник. Многогранник, гранями которого являются n-угольники A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называется усеченной пирамидой.
Вокруг нас много примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной пирамиды,.клавиши клавиатуры и другие предметы.
N-угольники A1A2…An и B1B2…Bn называются соответственно верхним и нижним основанием. Четырехугольники A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называются боковыми гранями.
Отрезки A1B1,…, AnBn называются боковыми рёбрами усеченной пирамиды.
Усеченную пирамиду обозначают так A1A2…AnB1B2…Bn. Возьмем на верхнем основании произвольную точку C и из этой точки опустим перпендикуляр на нижнее основание. Этот перпендикуляр называется высотой усеченной пирамиды.
Боковые грани усеченной пирамиды – это трапеции.
Как и в случае с пирамидой, усеченная пирамида тоже может быть правильной.
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.
Основаниями усеченной пирамиды являются правильные многоугольники, а боковые грани – равнобедренные трапеции.
Высоты этих трапеций называются апофемами.
Объединение боковых граней называется боковой поверхностью усеченной пирамиды, а объединение всех граней называется полной поверхностью усеченной пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней.
А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.
А теперь порешаем.
Задача. Стороны оснований правильной усеченной четырехугольной пирамиды равны 3см и 9см. Высота пирамиды равна 4см. Найти площадь боковой поверхности.
Решение.
Решим еще одну задачу.
Задача. Пирамида пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и высота пирамиды делятся этой плоскостью на
Что и требовалось доказать.
Решим еще одну задачу.
Задача. Правильная треугольная пирамидас высотой
Подсказка: при решении этих задач вы должны вспомнить, какие треугольники подобны и свойства подобных треугольников.
Выполните тест
Тест. Усеченная пирамида
Вопрос 1
Закончите фразу:
Боковые грани усеченной пирамиды - ....
Вопрос 2
Выберите верные высказывания:
- Усеченная пирамида называется правильной, если она получена сечением - правильной пирамиды плоскостью, параллельной основанию.
- Основания правильной усеченной пирамиды - трапеции
- Основания правильной усеченной пирамиды - правильные n-угольники
- Боковые грани правильной усеченной пирамиды - равнобедренные трапеции
Вопрос 3
Выберите верное утверждение:
- Площадь боковой поверхности правильной усеченной пирамиды равна произведению суммы периметров основания на высоту.
- Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на высоту.
- Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на апофему.
- Площадь боковой поверхности правильной усеченной пирамиды равна произведению суммы периметров основания на апофему.
Вопрос 4
Укажите плоскость, которая будет верхним основанием усеченной пирамиды:
A1A2....An
B1B2....Bn
A1B1B2A2
Вопрос 5
Укажите плоскость, которая будет нижним основанием усеченной пирамиды:
A1A2....An
B1B2....Bn
A1B1B2A2
Вопрос 6
Укажите плоскость, которая будет боковой гранью усеченной пирамиды:
A1A2....An
B1B2....Bn
A1B1B2A2
Вопрос 7
Стороны оснований правильной усеченной четырехугольной пирамиды ABCDA1B1C1D1 равны 3 см и 9 см. Высота пирамиды равна 4 см. Найти площадь боковой поверхности. В ответ запишите только число без единиц измерения. Например, 25
Вопрос 8
Пирамида пересечена плоскостью, параллельной основанию. Укажите верное утверждение.
- боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части
- боковые ребра и высота пирамиды делятся этой плоскостью на равные части.
Вопрос 9
Сколько углов имеет боковая грань усеченной пирамиды?
Вопрос 10
Усеченная пирамиды имеет 16 вершин. Сколько сторон у каждого из оснований этой пирамиды?
УРОК №17
21 .10.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «РЕШЕНИЕ ЗАДАЧ»
Для решения задач по теме необходимо вспомнить:
- какой многогранник называется усечённой пирамидой?
- вспомнить элементы усечённой пирамиды: основания (верхнее, нижнее), высота, апофема, центры пирамиды и как их можно определить.
- знать формулы боковой и полной поверхности пирамиды
-знать формулы теоремы Пифагора, свойства правильного треугольника.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?
Решение
Поскольку в пирамиде все боковые грани равны, то и площади их будут равны. Знаем, что площадь боковой грани на 15 меньше площади основания, значит она равна 27. В пятиугольной пирамиде боковых граней 5.
Таким образом, площадь полной поверхности равна 27∙5+42 = 177.
Ответ: 177
Задание 2. В правильной пирамиде высота боковой грани равна 10, а в основании лежит квадрат со стороной 4. Чему равна площадь боковой поверхности?
Решение
Боковая грань пирамиды – это треугольник. Все боковые грани этой пирамиды равны между собой, так как пирамида правильная. Вычислим площадь треугольника: ½∙4∙10=20.
В основании пирамиды лежит квадрат, значит боковых граней будет 4. Таким образом, площадь боковой поверхности равна 4∙ 20=80.
Ответ: 80
№ 268
Дано: MABCD - правильная пирамида, А1В1С1 || АВС, МО1 : O1O = 1 : 2, NK - апофема, NK = 4 дм, Syc.пиp. = 186 дм.
Найти: ОО1 - ?
Решение: Рассмотрите ΔМКО. Так как NO1 || KO, то МО11 : МО = O1 N : OK, значит, стороны В1 С1 : ВС = МО1 : МО. В1 С1 = 1 : 3. Пусть В1 С1 = х, ВС = 3х. Имеем
(не удовлетворяет условию задачи); В1 С1 = 3 (см), NО = 1,5 (см); ВС = 9 (см), ОК = 4,5 (см); KF = OK – NO1 = 3. Из ΔKNF по теореме Пифагора
(Ответ: √7 дм.)
№ 269.
Дано: АВСА1 В1 С1 — усеченная пирамида. АВ = ВС = АС = 4 см; A1 B1 = B1 C1 = A1 C1 = 2 см; АА1 = 2 см. Найти: МК- ? A\F\ - ?
Решение: Пусть О и О1 - центры оснований пирамиды.
1) Из ΔАВС имеем: АВ = R√3, R = АО.
2) Из ΔА1 B1 C1 находим
![]()
3) EK = ОK - OE, ОЕ = O1 М, отсюда
5) Из ΔМЕК имеем: МК2 =МЕ2 +ЕК2 МК =
= (Ответ: ![]() )
)
ЗАДАНИЕ: выполнить самостоятельно
Вариант I
1. Из данных утверждений выберите верное: а) все ребра правильной пирамиды равны; б) площадь поверхности пирамиды равна половине произведения периметра основания на апофему; в) боковые грани усеченной пирамиды - трапеции; г) утверждения a-в не верны.
2. Найдите площадь боковой поверхности пирамиды, все грани которой наклонены к основанию под углом 60°, а в основании лежит прямоугольный треугольник с катетами 3 см и 6 см.
а) 9 см2, б) 10 см2, в) 12 см2, г) другой ответ.
3. В правильной четырехугольной пирамиде сторона основания равна 5 см, а плоский угол при вершине пирамиды 60°. Найдите боковое ребро пирамиды
4. В основании пирамиды SABC лежит равнобедренный треугольник ABC, в котором ВС = 12 см, а АВ = АС = 10 см. Найдите площадь сечения ASM, если оно перпендикулярно плоскости основания, а все боковые ребра пирамиды равны 10 см.
а)
б)
в) 31 см2, г) другой ответ.
5. Боковые ребра пирамиды SABC равны между собой. SD - высота пирамиды. Точка D лежит внутри ΔABC. ТреугольникABC:
а) прямоугольный;
б) остроугольный;
в) тупоугольный;
г) недостаточно данных.
6. Найдите площадь диагонального сечения правильной усеченной четырехугольной пирамиды, если ее высота равна √2 см, а стороны основания 1 см и 4 см.
а) 10 см2, б) 2,5 см2, в) 5 см2, г) другой ответ.
УРОК № 15 - 16
17.10.2022г.
ГРУППА 303. МАТЕМАТИКА. ТЕМА «Правильная ТРЕУГОЛЬНАЯ ПИРАМИДА»
Правильная пирамида – это пирамида, основанием которой является правильный
многоугольник, а вершина фигуры проецируется в центр ее основания.
Самые
распространенные разновидности правильных пирамид: треугольная, четырехугольная
и шестиугольная. Рассмотрим их подробнее.
Правильная треугольная пирамида
Основание –
правильный/равносторонний треугольник ABC.
- Боковые грани – одинаковые
равнобедренные треугольники: ADC, BDC и ADB.
- Проекция вершины D на
основание – точка O, которая является точкой пересечения
высот/медиан/биссектрис треугольника ABC.
- DO – высота пирамиды.
- DL и DM – апофемы,
т.е. высоты боковых граней (равнобедренных треугольников). Всего их три
(по одной на каждую грань), но на рисунке выше изображено два, чтобы не
перегружать его.
- ⦟DAM = ⦟ DBL = α (углы между боковыми ребрами и
основанием).
- ⦟DLB = ⦟DMA = β (углы между боковыми гранями и
плоскостью основания).
- Для такой пирамиды верно
соотношение:
AO:OM = 2:1 или BO:OL = 2:1.
Примечание: если у правильной треугольной
пирамиды все ребра равны, она также называется правильным тетраэдром.
Свойства правильной
пирамиды
1. Все боковые ребра фигуры равны.
Другими словами вершина пирамиды находится на одинаковом расстоянии от всех
углов ее основания.
2. Угол между всеми боковыми ребрами и
основанием одинаковый.
3. Все грани наклонены к основанию под
одним и тем же углом.
4. Площади всех боковых граней равны.
5. Все апофемы равны.
6. Вокруг пирамиды можно описать сферу, центром которой будет точка пересечения
перпендикуляров, проведенных к серединам боковых ребер.
7. В пирамиду можно вписать сферу, центром которой
будет точка пересечения
.Тетраэдр
Частным
случаем правильной треугольной пирамиды является тетраэдр. Тетраэдр
- это правильный многогранник (правильная треугольная пирамида) у которой все
грани являются правильными треугольниками. У тетраэдра:
1.Все грани
равны
4 грани, 4
вершины и 6 ребер
Все
двугранные углы при рёбрах и все трёхгранные углы при вершинах равны
- Медиана тетраэдра - это отрезок, соединяющий
вершину с точкой пересечения медиан противоположной грани (медиан
равностороннего треугольника, противолежащего вершине)
- Бимедиана тетраэдра - это отрезок, соединяющий
середины скрещивающихся рёбер (соединяющий середины сторон треугольника,
являющегося одной из граней тетраэдра)
- Высота тетраэдра - это отрезок, соединяющий
вершину с точкой противоположной грани и перпендикулярный этой грани (то
есть является высотой, проведенной от любой грани, также совпадает с
центром описанной окружности).
- Тетраэдр обладает следующими свойствами:
- Все медианы и бимедианы
тетраэдра пересекаются в одной точке
- Эта точка делит медианы в
отношении 3:1, считая от вершины
- Эта точка делит бимедианы
пополам
Задача 2. В правильной треугольной пирамиде сторона основания 2√3, а высота равна 7 см. Найти угол наклона бокового ребра к плоскости основания
Дано:
АВ =ВС =АС = 2√3 Решение:
DN =7 см Высота
перпендикулярна плоскости основания, поэтому
∆ DNK-
Найти угол DKN -? Прямоугольный. А поэтому
NK/ DN = tg DKN
BK – высота, биссектриса и медиана треугольника АВС. В
точке N делится в отношении 2:1. ВК
находим из прямоугольного треугольника АВК по теореме Пифагора:
ВК = √АВ 2– АК2
= (2√3)2 –( √3)2 = √√32) = 3 см
NK = 1 см ; tg DKN =
тест «ПРАВИЛЬНАЯ ПИРАМИДА»
Вопрос 1
В правильной
пирамиде 8 вершин. Сколько у нее ребер?
Вопрос 2
Дана
правильная треугольная пирамида PABC. Высота РО = 12. Радиус окружности,
описанной около основания равен 5. Найдите длину бокового ребра.
Вопрос 3
Дана
правильная треугольная пирамида PABC. Высота РО = 12. Радиус окружности,
описанной около основания равен 6. Найдите длину стороны основания. Значение
квадратного корня из 3 считайте равным 1,7. Целую часть от дробной отделяйте
запятой!
Вопрос 4
Дана
правильная треугольная пирамида PABC. Боковое ребро равно 10, а сторона
основания 16. Найдите длину апофемы.
Вопрос 5
Дана
правильная треугольная пирамида PABC. Боковое ребро равно 10, а сторона
основания 16. Найдите площадь ее боковой поверхности.
Вопрос 6
Дана
правильная четырехугольная пирамида PABCD. Сторона основания равна 4
, а боковое
ребро равно 5. Найдите высоту пирамиды.
Вопрос 7
Дана
правильная четырехугольная пирамида PABCD. Сторона основания равна 4
, а боковое
ребро равно 5. Найдите апофему пирамиды. Результат округлите до десятых.
Вопрос 8
Дана
правильная четырехугольная пирамида PABCD. Сторона основания равна 8, а высота
равна 3. Найдите площадь ее боковой поверхности.
Вопрос 9
Дана
правильная четырехугольная пирамида PABCD. Сторона основания равна 8, а высота
равна 3. Найдите площадь ее полной поверхности.
Вопрос 10
Дана
правильная четырехугольная пирамида PABCD. Сторона основания равна 8, а высота
равна 3. Найдите тангенс двугранного угла пирамиды при ребре основания.
УРОК № 13-14
14.2022г. Группа 303. МАТЕМАТИКА. ТЕМА «ПРАВИЛЬНАЯ ПИРАМИДА»
Учебник: Геометрия. 10-11 классы: учеб.для общеобразоват. учреждений: базовый и профильный уровни/ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.].-20-е изд.- М.: Просвещение,2011.
Мы продолжаем с Вами изучать раздел геометрии «Многогранники».
-Вспомним , какие фигуры стереометрии мы уже изучили? (параллелепипед, призма)
- Вспомним определение этих фигур
Сегодня на уроке познакомимся с понятием пирамида и ее элементами, научимся изображать пирамиду в тетради и распознавать ее среди других тел.
Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольников
- Пирамидой называется многогранник, который состоит из плоского многоугольника-основания пирамиды, точки, не лежащей в плоскости основания-вершины пирамиды, и всех отрезков, соединяющих вершину пирамиды с точками основания.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.Пирамида называется n-угольной, если ее основанием является n-угольник.
Правильная треугольная пирамида называется также тетраэдром.
Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины
Теорема о площади боковой
поверхности правильной пирамиды:
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему d
Боковые грани правильной пирамиды – равные равнобедренные треугольники, снования которых – стороны основания пирамиды, а высоты равны апофеме –d
Sб = 1/ 2 P∙ d, а Sполн. = Sб. + Sосн.
ЗАДАНИЕ. ВЫПОЛНИТЕ ТЕСТ
Тест по теме «Пирамида»
1. Пирамидой называется многогранник, который состоит из …
а). 2-х плоских многоугольников и всех отрезков, соединяющих соответствующие точки этих многоугольников;
б). плоского многоугольника – основания пирамиды, точки не лежащей в плоскости основания и всех отрезков, соединяющих эту точку с точками основания;
в). Плоского многоугольника – основания пирамиды, точки- вершины пирамиды и отрезков, соединяющих вершину и основанием.
2. Основание n-угольной пирамиды это…
а) треугольник;
б) n-угольник;
в) 4-х угольник.
3. Вершина пирамиды- это…
а) точка, не лежащая в плоскости основания;
б) вершина многоугольника, лежащего в основании;
в) центр многоугольника, лежащего в основании.
4. Боковые рёбра пирамиды – это…
а) отрезки, соединяющие вершину пирамиды с вершинами основания;
б) отрезки, соединяющие вершину с серединами сторон снования;
в) отрезки, соединяющие вершины основания.
5. Боковые грани n-угольной пирамиды являются…
а) n-угольниками;
б) 4x- угольниками;
в) 3х- угольниками.
6. Высота пирамиды – это…
а) высота основания;
б) перпендикуляр, опущенный из вершины пирамиды на плоскость основания;
в) высота боковой грани.
7. У 5-ти угольной пирамиды вершин…
а) 1;
б) 5;
в) 6.
8. У 7-ми угольной пирамиды боковых граней…
а) 1;
б) 8;
в) 7.
9. У 8-ти угольной пирамиды боковых рёбер…
а) 16;
б) 8;
в) 9
10. Пирамида называется правильной, если…
а) её основание правильный многоугольник;
б) её основание квадрат, а основание высоты совпадает с центром этого многоугольника;
в) её основание правильный многоугольник и основание высота совпадает с центром этого многоугольника.
11. Осью пирамиды называются…
а) прямая, содержащая высоту пирамиды;
б) прямая, содержащая высоту основания пирамиды;
в) центр основания пирамиды.
12. Апофема – это…
а) высота пирамиды;
б) высота боковой грани;
в) высота основания.
13. Боковая поверхность правильной пирамиды равна…
а) произведению периметра основания на апофему;
б) произведению полупериметра основания на апофему;
в) произведению полупериметра основания на высоту пирамиды.
14. Полная поверхность пирамиды состоит из…
а) площади боковой поверхности и площади основания;
б) площади боковой грани и площади основания;
в) площади боковой поверхности и площади двух оснований..
15. В правильной 3-х угольной пирамиде апофема равна 5м, сторона основания 3м, тогда площадь боковой поверхности…
а) 45м2;
б) 15м2;
в) 22,5м2;
16. В правильной 4-х угольной пирамиде высота равна 9м, сторона основания 5м, тогда объём…
а) 75м3;
б) 112,5м3;
в) 45м3.
17.. Сторона основания правильной пятиугольной пирамиды 2м, площадь боковой поверхности 35м2. Апофема равна…
а) 17,5м;
б) 3,5м;
в) 7м..
18. У правильной пирамиды боковые грани являются…
а) равносторонними треугольниками;
б) прямоугольными треугольниками;
в) равнобедренными треугольниками.
19. У правильной пирамиды боковые ребра…
а) равны;
б) параллельны и равны;
в) параллельны..
20. В основании правильной четырехугольной пирамиды лежит…
а) трапеция;
б) квадрат;
в) прямоугольник..
21. Треугольная пирамида, у которой все ребра равны называется…
а) октаэдром;
б) тетраэдром;
УРОК № 11-12
14.10.2022г. ГРУППА 303. ГЕОМЕТРИЯ ТЕМА "Пирамида и ее элементы"
n-угольной пирамидой называется многогранник, одна грань которого - произвольный n-угольник, а все остальные п граней - треугольники, имеющие общую вершину.
Общую вершину треугольных граней называют вершиной пирамиды, противоположную ей грань - основанием, а все остальные грани - боковыми гранями пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Перпендикуляр, опущенный из вершины пирамиды на плоскость ее основания, называют высотой пирамиды.
На рис. 253 изображен четырехугольную пирамиду SABCD; точка S - ее вершина, ABCD - основание; SA, SB, SC, SD - боковые ребра; АВ, ВС, CD, AD - ребра основания; SO - высота пирамиды.
Правильную треугольную пирамиду называют также тетраэдром. Сумму площадей всех боковых граней пирамиды называют площадью боковой поверхности пирамиды. Чтобы найти площадь всей поверхности пирамиды, нужно к площади Sбоков ее боковой поверхности прибавить площадь Sосн основания: S = Sб. + Sосн.
Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника (рис. 254).
ЗАДАНИЕ:
1. 1. Сколько граней, ребер, вершин имеет n-угольная пирамида?
2. 2. Каждое ребро тетраэдра равен 2 см. Найдите площадь поверхности тетраэдра.
3. 3. Постройте треугольную и четырехугольную пирамиды.
Площадь поверхности и объем пирамиды
Теорема. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра ее основания на апофему.
Доказательство:
Пусть а - сторона основания правильной n-угольной пирамиды (рис. 255). SH![]() BC, SH = m.
BC, SH = m.
Тогда площадь боковой грани правильной пирамиды равна ½ am, а площадь боковой поверхности Sб. = ½ а ∙m ∙n. Так 1/2аn = р, где р - полупериметр основания пирамиды, то Sб. = pm.
Объем любой пирамиды равен трети произведения площади ее основания на высоту: V = 1/3 Sосн ∙ H.
Задачи. 1. Найдите площадь боковой поверхности правильной треугольной пирамиды, если сторона основания равна 12 см, а апофема 10 см.
1. 2. Найдите площадь боковой поверхности правильной четырехугольной пирамиды, если сторона основания равна 16 см, а боковое ребро 10 см.
2. 3. Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 6 см, а высота 10 см.
Составьтет конспект (образец приведен в табл. 11).
Таблица 11
Пирамида | |
n-угольная пирамида - многогранник, одна грань которого - произвольный n-угольник, а все остальные п граней - треугольники, имеющие общую вершину | |
S - вершина пирамиды; ABCD - основание пирамиды; ASAB, ASBC, ASCD, ASDA - боковые грани; SA, SB, SC, SD - боковые ребра; АВ, ВС, CD, AD - ребра основания; SO - высота, SO | |
Основание правильной пирамиды - правильный многоугольник, а основание высоты - центр многоугольника, SF - апофема, SF Площадь боковой поверхности правильной пирамиды Sбоков = mp, где m - апофема, р - полупериметр основания. Объем пирамиды V = | |
Решение задач
1. 1. В основании пирамиды SABC, изображенной на рис. 256, лежит прямоугольный треугольник ABC (![]() C = 90°), AC = 3 см, ВС = 4 см. Вычислите объем пирамиды, если высота SA равна 5 см. (Ответ. 10 см3)
C = 90°), AC = 3 см, ВС = 4 см. Вычислите объем пирамиды, если высота SA равна 5 см. (Ответ. 10 см3)
1. 2. В основе ABCD правильной пирамиды SABCD лежит квадрат со стороной 10 см. Высота SO пирамиды равна 12 см. Найдите площадь поверхности и объем пирамиды. (Ответ. 360 см2, 400 см3)
2. 3. Основание пирамиды - прямоугольник со сторонами 3 см и 5 см. Высота пирамиды 10 см. Найдите объем пирамиды. (Ответ. 50 см3)
3. 4. Найдите объем правильной четырехугольной пирамиды, каждое ребро которой равно а. (Ответ. а3)
4. 5. Боковые ребра треугольной пирамиды попарно перпендикулярны и имеют длины 3 см, 4 см и 5 см. Найдите ее объем. (Ответ. 10 см3)
5. 6. В правильной четырехугольном пирамиде боковое ребро равно 10 см. Найдите:
а) высоту пирамиды, если диагональ основания равна 16 см;
б) апофему пирамиды, если сторона основания равна 12 см.
1. 7. Найдите объем правильной четырехугольной пирамиды, боковое ребро которой равно 12 см и образует с высотой пирамиды угол 30°.
2. 8. Одна из самых величественных сооружений древности - пирамида Хеопса - имеет форму правильной четырехугольной пирамиды, высота которой равна 150 м, а боковое ребро - 220 м. Найдите площадь основания пирамиды. (Ответ. 51800 м2)
3. 9. На рис. 257 изображен развертку четырехугольной пирамиды, в основании которой лежит квадрат со стороной 6 см, боковые грани пирамиды - правильные треугольники. Найдите высоту пирамиды и ее объем.
1. 1. Изучить формулы площади поверхности и объема правильной пирамиды.
2. 2. Решить задачи.
3. 1) Найдите площадь поверхности правильной четырехугольной пирамиды, каждое ребро которой равно а.
4. 2) В основании пирамиды лежит ромб с диагоналями 6 см и 8 см. Высота пирамиды равна 10 см. Найдите объем пирамиды.
5. 3) Найдите объем правильной четырехугольной пирамиды, диагональ основания которой равна 4 см, а боковое ребро образует с высотой пирамиды угол 45°.
ОТВЕТИТЬ НА ВОПРОСЫ
1. 1. Что называется n-угольной пирамидой?
2. 2. Какая пирамида называется правильной?
3. 3. Какие свойства правильной пирамиды вам известны?
4. 4. Чему равна площадь поверхности пирамиды?
5. 5. Чему равна площадь боковой поверхности правильной пирамиды?
УРОК № 9-10
10.10.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА «Призма. РЕШЕНИЕ ЗАДАЧ»
Призма — это многогранная объемная фигура,
которая состоит из двух одинаковых плоских многоугольников (основ),
находящихся в двух параллельных плоскостях, а другие грани (боковые грани)
- параллелограммы, что имеют общие стороны с этими многоугольниками.
|
|
Определение.
Боковые грани призмы - все остальные грани за исключением основ.
Определение.
Боковая поверхность призмы - совокупность всех боковых граней призмы.
Определение.
Поверхность призмы - это совокупность поверхностей двух оснований и
боковой поверхности.
Определение.
Боковое ребро призмы - общая сторона двух боковых граней.
Определение.
Высота - это перпендикуляр, который соединяет две основы призмы под
прямым углом.
Определение.
Диагональ основания призмы - это отрезок, соединяющий две не соседние
вершины, принадлежащие этой же основе.
Определение.
Диагональ боковой грани призмы - это отрезок, соединяющий две
противоположные вершины, лежащие на одной боковой грани однако принадлежат
различным основам.
Определение.
Диагональ призмы- это отрезок, соединяющий две вершины, лежащие в разных
плоскостях.
УРОК №6-7
03.10.2022г. ГРУППА 303. МАТЕМАТИКА. ТЕМА. «ПАРАЛЛЕЛЕПИПЕД. КУБ.»
Начнем с того, что узнаем, что такое параллелепипед.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
основание;
грани;
ребра;
диагонали;
диагонали граней;
высота.
Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Параллелепипед симметричен относительно середины его диагонали.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
На рисунке: ребро АА1 перпендикулярно основанию ABCD. АА1 перпендикулярна прямым АB и АD, которые лежат в плоскости основания
Свойства прямого параллелепипеда:
1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота
Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания
Объем прямого параллелепипеда
V = Sо*h
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
На рисунке: основание прямоугольного параллелепипеда ABCD; боковое ребро АА1 перпендикулярно АВСD; угол BAD = 90°
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5.В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7.Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота
Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро
Площадь поверхности
Sп.п = 2(ab+bc+ac)
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Применяем формулу:
d² = a² + b² + c²
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
d₁² = a² + b²
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
1. В кубе 6 граней, каждая грань куба — квадрат
2. Противолежащие грани параллельны друг другу.
3.Все углы куба, образованные двумя гранями, равны 90°.
4.У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
5.Диагонали куба равны.
6.Диагональ куба в √3 раз больше его ребра.
7. Диагональ грани куба в √2 раза больше длины ребра.
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
Объем куба через длину ребра a
V = a3
Площадь поверхности куба
S = 6a2
Периметр куба
P = 12a
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) - сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) - суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) - сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) - сумма длин всех ребер прямоугольного параллелепипеда.
Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X - сумма длин ребер).
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5∙8 + 8∙10 + 5∙10) ∙ 2 = 340 см2.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
D1B = √26
BB1 = 3
A1D1 = 4
Нужно найти длину ребра A1B1
Угол D = 90°. Против равных сторон лежат равные углы.
По теореме Пифагора:
BD12 = DD12 + BD2
BD2 = BD12 – DD12
BD2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD2 = AD2 + AB2
AB2 = BD2 - AD2 = (√17)2 — 42 = 1
A1B1 = AB.
Здачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
Решение
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD2 = AB2+AD2
BD2 = 42 + 62 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD12 = 52 + 25 = 77.
Самопроверка
Теперь потренируйтесь самостоятельно — верю, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AC1= 15
C1D1 = 3
B1C1= 12
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
1. прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
2. параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
3. основание прямоугольного параллелепипеда — прямоугольник;
4. три измерения прямоугольного параллелепипеда: длина, ширина, высота;
5. диагональ параллелепипеда равна сумме квадратов его измерений.
ЗАДАНИЕ:
СОСТАВЬТЕ КОНСПЕКТ СООБЩЕНИЯ,
УРОК №4-5
19.09.2022г. ГРУППА 303. МАТЕМАТИКА. Тема « Призма».
Давайте повторим ранее изученную тему «Многогранные углы. Многогранник»
1. Дайте определение многогранника.
Ответ: Многогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями.
Стороны граней называются ребрами многогранника, а концы ребер — вершинами многогранника.
2. Сформулируйте понятие правильного выпуклого многогранника.
Ответ: Выпуклый многогранник называется правильным, если все его грани — правильные одинаковые многоугольники и все многогранные углы при вершинах равны.
3. Существует 5 видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
4. Сформулируйте теорему Эйлера.
Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, доказательство которой Эйлер опубликовал в 1758 г.
Вершины + Грани - Рёбра = 2.
5. Изобразите выпуклый многогранник и укажите грани, ребра и вершины.
Ответ: Куб АВСДА1В1С1Д1, грани: АВСД, …., ребра: АВ, ВС,…, вершины: А, В, С, ….., Д1.
Сегодня мы будем знакомиться еще с одним видом многогранника – это «Призма».
Призма — это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани — параллелограммами.
Грани, которые находятся в параллельных плоскостях, называются основаниями призмы, а остальные грани — боковыми гранями призмы.
Рассматривая элементы призмы нельзя не обратить на свойства этой фигуры.
Даем определение каждому виду призмы. В зависимости от основания призмы бывают:
Четырёхугольная
Шестиугольные и др.
Призма с боковыми рёбрами, перпендикулярными её основаниям, называется прямой призмой, как в предыдущих рисунках.
Прямая призма называется правильной, если её основания — правильные многоугольники.
Расстояние между основаниями призмы называется высотой призмы.
Высота прямой призмы совпадает с боковым ребром.
Высота наклонной призмы — это перпендикуляр, проведенный между основаниями призмы. Часто перпендикуляр проводят с одной из вершин верхнего основания.
Без дополнительных условий невозможно определить, в какую точку проектируется высота наклонной призмы.
Ответьте, пожалуйста на вопрос: «Что собой представляет развёртка призмы?»
.А теперь ознакомимся с формулами площади боковой поверхности и полной поверхности призмы, так же и для разных видов призм.
Площадь поверхности геометрической фигуры измеряется в квадратных единицах. Очень часто используется в повседневной жизни, в строительстве, на производствах. Например, нужно вам покрасить комнату, зная сколько краски используется на кв. метр, и площади стен комнаты легко можно вычислить, сколько всего вам нужно купить краски.
Различают два вида площадей поверхности тел: Sбок - площадь боковой поверхности тела, и Р - площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы (высота = боковому ребру).
Sбок = ph=pl
р - периметр основания;
h - высота;
l - боковое ребро.
IV. Решение задач
Задача 1
По стороне основания (a
Дано:
ABCA1 B1 C1
Найти: Sполн.
Sп =3ab + 2a2√3/4
Боковая поверхность призмы равна: Sп =3ab + 2a2√3/4
Задача 2
Боковая поверхность правильной четырехугольной призмы 32 м2, а полная поверхность — 40 м2. Найдите высоту.
Дано:
АБСДА1 Б1С1 Д1
S б = 32м2 ; Sп =40м2
Найти:
Решение:
Sп = Sб + 2Sосн. отсюда имеем: Sосн = Sп -Sб /2 = 40 -32 /2 = 4 м2
Так как в основании находится квадрат, то сторона квадрата равна:
Sб = ph=4ah
Ответ: 4 м.
V. Самостоятельная работа
Задача1.
Найдите боковое ребро правильной четырёхугольной призмы, если сторона её основания равна 30, а площадь поверхности равна 2760
Задача2
Основание прямой треугольной призмы служит прямоугольный треугольник с катетами 7 и 21. Высота призмы равна 15. Найти площадь её поверхности.
Задание 1.
Найдите для каждой картинки пару 1, 2, 3, 4, 5
Задание 2
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
2) отрезок
3) точка
4) четырехугольник
УРОК № 1-3
05.09.2022г. ГРУППА 303 МАТЕМАТИКА Тема урока: « Понятие многогранника. Призма»
Прежде чем приступить к изучению нового материала мы должны вспомнить:
1. Чему равна сумма углов в треугольнике?
2. Сформулируйте свойство углов при основании равнобедренного треугольника.
3. Чему равны острые углы равнобедренного прямоугольного треугольника?
4. Сформулируйте свойство катета, лежащего против угла в 300?
5. Что называют углом между прямой и плоскостью?
6. Сформулируйте определение прямой перпендикулярной плоскости.
какую фигуру мы называем параллелепипедом?
7. Какую фигуру мы называем прямоугольным параллелепипедом?
Какой многоугольник называется правильным?
Сегодняшний урок посвящен введению в увлекательный раздел геометрии – теорию многогранников. Чем привлекательны многогранники? Они обладают богатой историей, которая связана с таким знаменитыми учеными древности, как Пифагор, Евклид, Архимед.
Многогранники были известны в Древнем Египте и Вавилоне. Мы познакомимся с вами с понятие многогранника и узнаем, какой многогранник называется призмой, а ещё много интересных фактов, связанных с многогранниками
В главе первой мы рассмотрели тетраэдр и параллелепипед: тетраэдр – это поверхность, составленная из четырёх треугольников ,а параллелепипед – это поверхность, составленная из шести параллелограммов ). Каждая из этих поверхностей ограничивает некоторое геометрическое тело, отделяет это тело от остальной части пространства.
Поверхность составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.
Рассмотрим примеры многогранников.
Тетраэдр и параллелепипед мы с ними уже знакомы. Вот ещё один многогранник – октаэдр, он состоит из 8 треугольников. .
А теперь открываем учебники на странице 57 и
Прочитайте учебник (стр. 57 абзац 3) и ответьте в тетради на вопросы:
1. Что называют гранями многогранника?
2. По рисунку посчитайте число граней данного многогранника.![]()
3. Что называют рёбрами многогранника?
4. По рисунку посчитайте число рёбер данного многогранника.
5. Что называют вершинами многогранника?
6. По рисунку посчитайте число вершин данного многогранника.
7. Что называют диагональю многогранника?
Многогранники бывают выпуклыми и невыпуклыми.
Большой вклад в изучение многогранников внёс Леонард ЭЙЛЕР
ЭЙЛЕР Леонард (1707-83), математик, механик, физик и астроном. По происхождению швейцарец. В 1726 был приглашен в Петербургскую АН и переехал в 1727 в Россию. Эйлер — ученый необычайной широты интересов и творческой продуктивности, автор св. 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки, оказавших значительное влияние на развитие науки.
Он ввёл характеристику, которая в последствие стала называться Эйлеровой, а заключается она в нахождение значения следующего выражения В-Р+Г.
. С одним из таких многогранников, мы сейчас подробнее и познакомимся.
Запомните ! Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники, при n больше 6.
Призма.
Рассмотрим два равных многоугольника А1А2…Аn и В1В2... Вn, расположенных в параллельных плоскостях ![]() и
и![]() так, что отрезки А1В1, А2В2, ..., АпВп, соединяющие соответственные вершины многоугольников, параллельны. Каждый из n четырехугольников
так, что отрезки А1В1, А2В2, ..., АпВп, соединяющие соответственные вершины многоугольников, параллельны. Каждый из n четырехугольников
A1A2B2B1 ,A2A3B3B2 ,… AnA1B1Bn (1)
является параллелограммом, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике А1А2В2В1 стороны А1В1 и А2В2 параллельны по условию, а стороны А1 А2 и В1В2 — по свойству параллельных плоскостей, пересеченных третьей плоскостью (п.11).
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2... Вn , расположенных в параллельных плоскостях, и п параллелограммов (1), называется призмой.
Многоугольники АгА2... Аn и ВгВ2... Вn называются основаниями, а параллелограммы (1) - боковыми гранями призмы. Отрезки А1В1, А2В2, ..., АnВn называются боковыми ребрами призмы. Эти ребра как противоположные стороны параллелограммов (1), последовательно приложенных друг к другу, равны и параллельны.
Призму с основаниями А1А2. ..Ап и В1В2...Вп обозначают А1А2...АnВ1В2...Вn и называют n-угольной призмой.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае — наклонной. Высота прямой призмы равна ее боковому ребру.
Прямая призма называется правильной, если ее основания — правильные многоугольники.
А если в его основании квадрат?
(Правильной четырёхугольной призмой.)
А теперь решаем задачи на изученный вами материал.
Пока ученики решают, учитель выдаёт им образцы изображения призм.
![]()
3. Решение задач.
№219.
В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.
№220.
Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда равна 10 см. Найдите большую диагональ параллелепипеда.
Попробуйте ответить на вопросы
по теме «Многогранники»
1. Многогранник, состоящий из плоского многоугольника и точки, не
принадлежащей плоскости основания и всех отрезков, что соединяют вершину с точкой основания.
2. Два плоских многоугольника, из которых состоит призма.
3. Полуплоскости, образующие двугранный угол.
4. Сторона грани многогранника
5. Основание параллелепипеда.
6. Призма, основанием которой является параллелограмм.
7. Правильная треугольная пирамида.
8. Отрезок, соединяющий две вершины, что не принадлежат одной грани.
(Диагональ)
9. Основание прямоугольного параллелепипеда.
10. Правильный многогранник, грани которого квадраты











































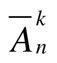
















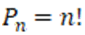




































































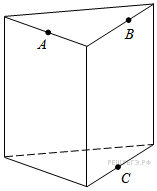













































































































Комментариев нет:
Отправить комментарий