10.01.2022г. ГРУППА 206. МАТМАТИКА ТЕМА «Комбинаторика - основные понятия и формулы. Перестановки, размещения, сочетания. Основные понятия и формулы»
Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Общее число N способов, которыми можно выбрать по одному элементу из каждой группы и расставить их в определенном порядке (то есть получить упорядоченную совокупность ( a b c d), равно:
N = n1 ∙ n2 ∙… nn
Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?
Решение
Первая монета имеет n1 = 2 альтернативы – либо орел, либо решка. Для второй монеты также есть n2 = 2 альтернативы и т.д., т.е. n1 = n2 =n3 =23 =8
Искомое количество способов:
N =n1 +n2 + …nn
Правило сложения
Если любые две группы A1 и A2 не имеют общих элементов, то выбор одного элемента или из A1 , или из A2…или из Ak можно осуществить способами.
N = n1 +n2 + …nk
Пример 2
На полке 30 книг, из них 20 математических, 6 технических и 4 экономических. Сколько существует способов выбора одной математической или одной экономической книги.
Решение
Математическая книга может быть выбрана n1 =20 способами, экономическая – n2 =4 способами.
По правилу суммы существует N способа выбора математической или экономической книги. N = n1 +n2 =20 + 4 =24
Размещения и перестановки
Размещения – это упорядоченные совокупности элементов, отличающиеся друг от друга либо составом, либо порядком элементов.
Размещения без повторений, когда отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется последовательным выбором без возвращения, а его результат – размещением без повторений из n элементов по k .
Число различных способов, которыми можно произвести последовательный выбор без возвращения элементов из генеральной совокупности объема , равно:
Расписание дня состоит из 5 различных уроков. Определите число вариантов расписания при выборе из 11 дисциплин.
Решение
Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и порядком следования. поэтому:
Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из n элементов равно
Пример 4
Сколькими способами можно рассадить 4 человек за одним столом?
Решение
Каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
Размещения с повторениями, когда отобранный элемент перед отбором следующего возвращается в генеральную совокупность. Такой выбор называется последовательным выбором с возвращением, а его результат - размещением с повторениями из n элементов по k.
Общее число различных способов, которыми можно произвести выбор с возвращением k элементов из генеральной совокупности объема n, равно
An-k = nk
Пример 5
Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?
Решение
Каждый из способов распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком. Так как одном этаже может выйти как один, так и несколько пассажиров, то одни и те же пассажиры могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 7 элементов по 6:
Сочетания
Сочетаниями из Cn элементов по k называются неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним элементом.
Пусть из генеральной совокупности берется сразу несколько элементов (либо элементы берут последовательно, но порядок их появления не учитывается). В результате такого одновременного неупорядоченного выбора n элементов из генеральной совокупности объема k получаются комбинации, которые называются сочетаниями без повторений из n элементов по k .
Число сочетаний из n элементов по k равно: Cnk = ![]()
Пример 6
В ящике 9 яблок. Сколькими способами можно выбрать 3 яблока из ящика?
Решение
Каждый вариант выбора состоит из 3 яблок и отличается от других только составом, то есть представляет собой сочетания без повторений из 9 элементов:
Количество способов, которыми можно выбрать 3 яблока из 9:
Пусть из генеральной совокупности объема выбирается элементов, один за другим, причем каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность. При этом ведется запись, какие элементы появились и сколько раз, однако порядок их появления не учитывается. Получившиеся совокупности называются сочетаниями с повторениями из n элементов по k. Число сочетаний с повторениями из n элементов по k:
Cn-k = Ck n+k-1
На почте продают открытки 3 видов. Сколькими способами можно купить 6 открыток?
Решение
Это задача на отыскание числа сочетаний с повторениями из 3 по 6
N = C3-6 = C 63 +6 -1 =C86 =![]() =
= ![]() =28
=28
Разбиение множества на групп
Пусть множество из различных элементов разбивается на k групп так, то в первую группу попадают n1 элементов, во вторую n2- элементов, в k-ю группу – nk элементов, причем n1+n2+…nk =n
Такую ситуацию называют разбиением множества на k группы.
Число разбиений на групп, когда в первую попадают элементов, во вторую - элементов, в k-ю группу - элементов, равно: N (n1 n2 ... nk) =![]()
Пример 8
Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?
Решение
Здесь n =16 k =3 n1 =5 n2 = 7 n3 =4
Число разбиений на 3 подгруппы:
ВЫВОД
1. Сделайте конспект сообщения, выписав определения и формулы.
2.Решите задачу: Какими способами можно рассадить 6 человек за одним столом?

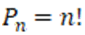








Комментариев нет:
Отправить комментарий