ГРУППА 205 ФИЗИКА Тема «Свободные колебания» (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
матического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту h, определяется по формуле:
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
ЗАДАНИЕ:
1. Сделайте конспект, ответив на вопросы:
А) Какие колебания называются свободными? Приведите примеры.
Б) Какие условия необходимы для возникновения колебаний?
В) Что такое математический маятник?
Г) Запишите формулы периода, частоты, циклической частоты, максимальной скорости и максимального ускорения для колебаний математического маятника и пружинного маятников .





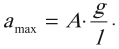
















Комментариев нет:
Отправить комментарий